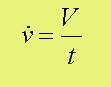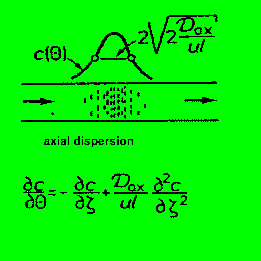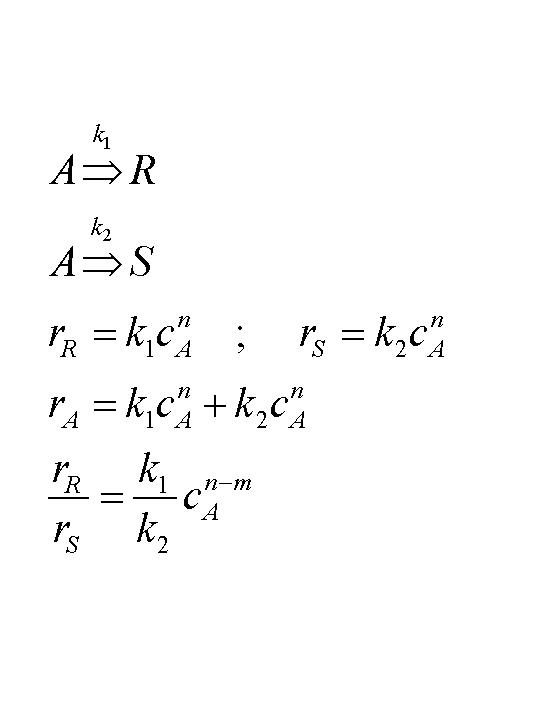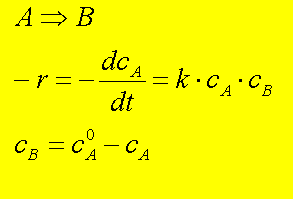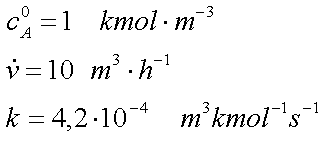Fortbildung für technisch interessierte Laien: 'Was ist chemische
Reaktionstechnik?' - Teil 3
zurück zu Teil 1
zurück zu Teil 2
zur
Homepage des Autors
Mal ganz logisch gedacht: die Möglichkeit, mit anderen
'Molekülkügelchen' zu reagieren hängt doch davon ab, wie lange
unsere Reaktandenmoleküle im Reaktionsraum vorhanden sind ('verweilen').
Im AIK ist das einfach: 'da kommt ja keiner zwischenzeitlich heraus!'
die 'Verweildauer' ist hier einfach die Zeit: 'wie lange der AIK betrieben
wird'. Anders bei den kontinuierlichen (durchströmten) Typen. Hier
schwirren die 'Kügelchen' einfach jedes eine bestimmte Zeit im
Reaktionsraum herum und die, die es sozusagen 'erwischt', daß sie dem
Auslauf (zu) nahe kommen, werden hinausgetragen. Also das Verweilzeitverhalten
einzelner Fluidelemente im Reaktionsraum ist individuell, damit wird die
Verweildauer zu einem statistischen Problem ( gerade wie z.B. beim
Publikumsverkehr in einem U-Bahnhof u.v.a.). Nun brauchen wir uns da nicht
groß zu verrenken: statistische Populationsverteilungen sind in
Naturwissenschaften und Technik 'Gang und Gebe'. Ein sehr 'schönes'
Beispiel ist z.B. die Charakterisierung einer Regelstrecke in der
Regelungstechnik mithilfe der 'Strecken-Sprungantwort'. Dies ist nichts anderes
als die Aufnahme einer ('statistischen') Summenkurve. Und im Grunde genommen
ist diese Prozedur ein exaktes Analogon zur Aufnahme einer Verweilzeitkurve in
der Reaktionstechnik. In beiden Fälllen wird 'die Zeitcharakteristik'
eines Obejkts ermittelt, mathematisch spricht man von
'Übertragungsfunktionen'.
Wir sprechen also in unserem
reaktionstechnischen Fall einfach von der 'Verweilzeitdichteverteilung' im
Reaktionsraum und wenden Methoden der statistischen Mathematik auf das Problem
an. Bei der Beschreibung von statistischen Verteilungsfunktionen werden immer
sogenannte Summenkurven der
Verteilungfunktion oder sogenannte Spektralkurven derselben betrachtet, die
übrigens als Differential und Integral mathematisch miteinander
'verknüpft' sind.
Wichtig ist nur, zu realisieren, daß
diese Verweilzeitverteilung zunächst keine chemische Reaktion
'beinhaltet'.
Man spricht hier übrigens von einem hydrodynamisch (=
strömungstechnisch) eingefahrenen Zustand, also der Apparat wird schon
'strömungstechnisch stationär' betrieben. Was letztlich dann
untersucht wird, ist, wie der Apparat 'konzentratinsmässig anläuft'.
Die im Apparat 'eingstellte Strömungstechnik' bestimmt z.B. auch die
sogenannte Hydrodynamische Verweilzeit 'tau', gegeben durch den Quotienten
'Volumen/Volumenstrom' (was ja die Dimension einer Zeit ergibt). Diese ist
sozusagen der 'Balken' für die mittlere Verweilzeit um die sich die
statistischen Verweilzeiten 'herumscharen' (in Form der Verteilungskurve), -
natürlich etwas vereinfacht ausgedrückt.
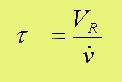 mit:
mit:
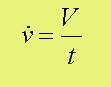
Die zu beobachtende Verteilungsfunktion ist einzig und alleine
durch das 'Strömungsmuster' im Apparat geprägt, und wenn wir hier
'etwas umfangreicher Formeln zulassen' würden, könnten wir zeigen,
daß die experimentell beobachteten Verteilungs-Funktionen weitgehend mit
denen übereinstimmen, die wir erhalten, wenn wir eine Stoffstrombilanz des
Apparats in Form einer Differentialgleichung ansetzen und mathematisch
lösen. Ja es ist sogar so, daß die Unterschiede zwischen Berechnung
und Experiment genau das 'reale Verhalten' des Apparats charakterisieren. Wenn
wir den für Idealreaktoren rechnerisch erhaltenen Verlauf der
Verweilzeitfunktion dem jeweiligen Reaktortyp zuordnen, haben wir die Charakteristik der Makrovermischung (v.a.
Grad der Rückvermischung) in diesem Reaktortyp 'kategorisiert'. Wenn wir
die Abweichungen von dieser 'Idealfunktion' betrachten, beurteilen wir die
Qualität der Makrovermischung
(Grad der Idealität).
|
nochmals:
Verweilzeitverteilungen informieren uns über die Charakteristik und die
Qualität des Makrovermischungsverhaltens von
Reaktoren |
|
Wie oben bereits angedeutet, werden zur experimentellen Ermittlung von
Verweilzeitkurven Tracermarkierungen vorgenommen. Für uns als Beobachter
sind natürlich Farbtracer sehr 'instruktiv', weil wir da etwas sehen
können. Nun spicht man bei der Aufnahme des Verlaufs von
Übertragungsfunktionen von Objekten von der Aufgabefunktion auf das Objekt und von dem Übertragungsverhalten des
'Übertragungsglieds' (Objekts) und der daraus sich ergebenden
Antwortfunktion.
Als Aufgabefunktionen kommen in der Praxis folgende Funktionen vor, die
zugleich auch mathematisch beschreibbar sein sollen:
- Sprungfunktionen
- Nadelpulsfunktionen ('Dirac-Stoß')
- Periodische Funktionen (Sinus-, Dreiecks-, Rechtecks-Funktionen)
- stochastische Funktionen
Lassen Sie uns die Eigenschaften und Vor- sowie Nachteile der einzelnen
Methoden der 'Aufgabe von Erregerfunktionen' gleich bei der Besprechung der
verschiedenen Anwendungen diskutieren.
8.1.1) Sprungantworten ergeben Summenkurven
Welche der Idealreaktoren AIK, KIK, IR betrachten wir eigentlich ? Da
wir oben bereits festgestellt haben, daß ein AIK eigentlich ja kein
Verweilzeitspektrum hat, kommen nur KIK und IR und Schaltungen kontinuierlicher
Reaktoren in Frage.
Bei der Sprungantwort wird der Tracer zu einem
bestimmten Zeitpunkt 'schlagartig' in voller Höhe zugegeben und seine
Zuflußmenge 'verbleibt auf diesem Pegel', - dies nennt man eine
'Sprungfunktion'. Die Antwortkurve wird in einer charakteristischen Form
ansteigen und schließlich auf dem gleichen Pegel wie die Sprungfunktion
'landen'. Wenn wir bei der Auswertung etwas eleganter vorgehen, normieren wir
das Tracer-Mengen-Signal, indem wir den aktuell beobachteten Wert
(Konzentration, Masse, Signalwert o.ä.) durch den 'Vollwert' der
Sprungfunktion dividieren. Damit bewegt sich der Signalverlauf zwischen 0 und
1. Unsere Antwortkurve (Summenkurve der Verweilzeit) beginnt also mit 0 und
endet mit 1. Derartige Aufgabefunktionen lassen sich leicht bewerkstelligen.
Nachteile sind, daß bei der mathematischen Auswertung für das
Spektrum abgeleitet (differenziert) werden muß (hier kann 'Feinstruktur'
verlorengehen). Ein weiterer Nachteil kann eventuell der relativ hohe
Tracer-Verbrauch sein.
8.1.1. a.) Die Verweilzeitsummenkurve eines IR
Eigentlich müssten wir den Verlauf dieser Funktion durch
Überlegen 'zusammenkriegen' ! Wenn die Sprungfunktion schlagartig auf
vollem Pegel in das IR eintritt, wird sie dieses anschließend als
'scharfe Front' durchlaufen und genau die Hydrodynamische Verweilzeit 'tau'
benötigen, bis sie (die Front) am Reaktorende angelangt ist. Vergessen Sie
nicht, wir haben es ja mit einer idealen Pfropfströmung zu tun.
8.1.1. b.) Die Verweilzeitsummenkurve eines KIK
So ganz trivial ist die gedankliche Herleitung hier nicht mehr. Aber,
überlegen wir einmal, wenn nun der Tracerpegel am KIK-Eingang schlagartig
auf '1' ansteigt, wird er ebenso schlagartig mit dem ganzen Fluidvorrat im
Kessel verdünnt, - und das in vollständiger Rückvermischung. Es
wird also der Tracerpegel im KIK nicht sofort, aber doch stetig ansteigen, bis
er im KIK ebenfalls '1' erreicht hat. Nun, wir können den Anstieg ja
experimentell beobachten und auswerten. Wir werden feststellen, daß es
sich um eine aufsteigende Exponentialfunktion handelt. Genau das sagt uns auch
die mathematische Herleitung aus der Differenzialgleichung für die
Stoffstrombilanz des KIK. Dies ist ja auch irgendwie plausibel, denn bei fast
allen Lösungen von Differenzialgleichungen erhalten wir irgendwie geartete
E-Funktionen.
Ein experimenteller Verlauf der Aufnahme einer Summenkurve könnte
etwa so aussehen, wie in der vorliegenden gif-Animation sozusagen im 'Zeitraffer' gezeigt (übliche
Verweilzeiten werden etwas länger sein). (Achtung: zurück einfach mit
Browser-back)
|
Beim IR wandert
die Sprungfunktion innerhalb der (hydrodynamischen) Verweilzeit ('frontal')
durch das Rohr, beim KIK ist ein exponentieller Anstieg im Reaktor zu
beobachten, wobei das Ende '1' nicht schon innerhalb der (hydrodynamischen)
Verweilzeit tau erreicht wird. |
|
Wie das bei einem Farbtracer-Experiment aussehen könnte, soll uns
die folgende gif-Animation zeigen.
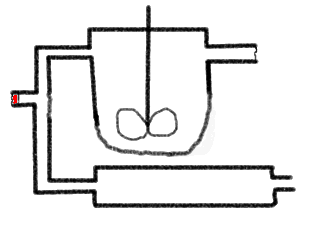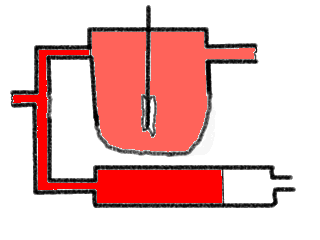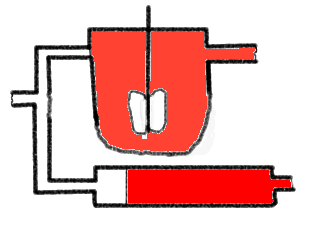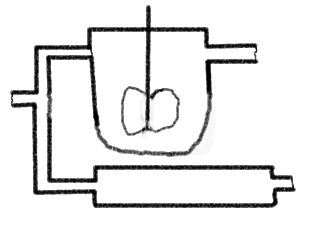
Die Abbildung zeigt eine Parallelschaltung eines KIKs und eines IR. Im
Zulauf wird eine Sprungfunktion eines roten Tracerfarbstoffs zugegeben. Man
sieht, wie die Front durch das Rohr wandert und wie die Farbe im KIK ansteigt,
bis sie 'voll rot' ist. Nach kurzer Zeit wird im Zulauf wieder schlagartig auf
'Null-Tracer' umgestellt und wir können den Vorgang sozusagen umgekehrt
beobachten. Diese umgekehrte Sprungantwortmethode wird
'Verdrängungsmarkierung' genannt, sie ist sozusagen die
'Ausverdünnungscharakteristik'. Für die etwas 'mässige'
Qualität der Farbzu- und -abnahme im KIK möchte ich mich
entschuldigen, - aber das ist übrigens gar nicht so einfach.
8.1.2.) Nadelpulsaufgaben ergeben die spektrale Verteilung (das
Spektrum) als Antwort
Zunächst einmal, was ist ein Nadelpuls oder auch 'Dirac-Stoß'
? Dieses Aufgabesignal wird im Idealfall als infinitesimal schmales und
unendlich hohes Signal definiert. Dies macht die praktische Verwendung des
Nadelpulses schwierig, denn es ist ja eigentlich nicht realisierbar. Aber auch
bei Anwendung möglichst schmaler und realisierbar hoher 'Nadeln' kann ein
ausreichendes Ergebnis erhalten werden. Das Nadelpuls-Signal erzeugt, und dies
ist mathematisch hergeleitet, die spektrale Antwort.
|
Sprungfunktionen
ergeben Summenkurven und Nadelpulsfunktionen ergeben Spektralkurven der
Verweilzeit. Summenkurven sind das Integral der Spektralkurven über die
Zeit von 0 bis unendlich. Spektalkurven ergeben sich durch Differenzieren der
Summenkurven. |
|
8.1.2.a.) Verweilzeitspektrum des IR
Diese Funktion können wir uns wieder leicht herleiten. Ein
Nadelpuls erreicht den Rohreintritt. Nun wird er mit der Pfropfströmung
und (per def. des IR) völlig nicht-rückvermischt durch das Rohr
'wandern'. Er ändert sich nicht in seiner Form und verlässt nach der
hydrodynamischen Verweilzeit wieder unverändert das Rohr. Nun, das ist ja
wenig dramatisch! Wir können aber mit der ganzen Information doch einiges
anfangen. Greifen wir einmal etwas auf nachfolgende Erörterungen vor. Wie
wird denn das Spektrum aussehen, wenn wir ein 'reales' Rohr vor uns haben, bei
dem wir teilweise Rückvermischung (und in diesem Fall auch
'Vorwärtsvermischung' in Axialrichtung, also ein teilweises Vorauseilen
von Fluidelementen ) haben ? Dann erhielten wir doch sicherlich eine
Spektralkurve von der Form einer Gauss'schen Glocke. Die Varianz dieser Glocke
ist dann ein Maß für die 'Realität' unseres Rohrs.
8.1.2.b.) Verweilzeitspektrum des KIK
Sollen wir uns die Sache leicht machen? Die Antwort des KIK auf einen
Nadelpuls ist das Spektrum. Das Spektrum ist die Ableitung der Summenkurve. Die
Ableitung einer aufsteigenden Exponentialkurve ist eine fallende
Exponentialkurve. Unsere Spektralkurve muß eine abfallende
Exponentialfunktion sein. Das ist auch plausibel. Wenn ein realer Nadelpuls in
den KIK gegeben wird, so ist das ja (im Vergleich zum Reaktorvolumen) eine
ziemlich geringe Stoffmenge. Diese wird nun im KIK stetig ausverdünnt,
wird immer kleiner und zum Schluß ist sie verschwunden, denn es kommt ja
nichts nach. Dieser abklingende Verlauf ist wegen der geringen Mengen
messtechnisch relativ schwierig zu erfassen. Deshalb ist die Nadelpulsmethode
beim KIK in der Praxis oft nicht so recht praktikabel. Wenn man aber in
pseudo-Echtzeitsimulationen des Vorgangs in Rechnern einfach den Trick anwendet
und das Ausgabesignal mit einem Verstärkungsfaktor versieht, dann kann man
das Spektrum ganz gut visualisieren. Dies soll in einer
gif-Animation einer Simulation (wieder 'im
Zeitraffer') gezeigt werden. (zurück mit Browser-back !!!)
Man sieht hier, daß der Nadelpuls eine 'reale' Breite hat und mehr
wie ein Rechteckpuls aussieht. Aber rein qualitativ kann man die spektrale
Abklingkurve erkennen. Diese ist aber - trotz angewandtem
Vertsärkungsfaktor - 'recht mickrig'.
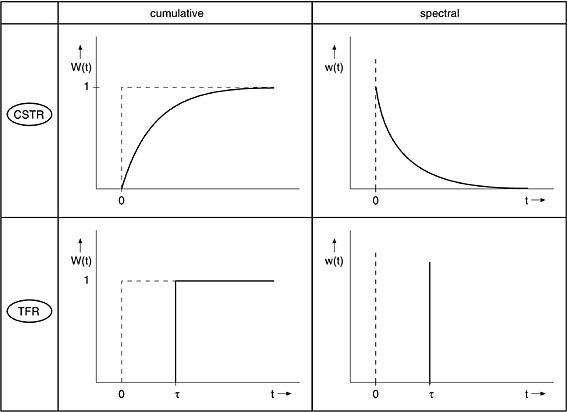
Wollen wir nochmals ein zusammenfassendes Bild über Summen- und
Spektralkurven für KIK und IR ansehen. Sie sollten anhand des Bildes
nochmals alles Besprochene rekapitulieren. (Hinweis engl. cumulative =
Summenkurve). Viel Erfolg !!
|
Die
Verweilzeitspektren der idealen Reaktoren zeigen uns deren
Makrovermischungs-Charakteristik. Sie zeigen die Grenzfälle der
Vollständigen Rückvermischung (im KIK) und der Vollständigen
Nicht-Rückvermischung (im IR). |
|
Da wir jetzt mit der Besprechung des Verweilzeitverhaltens der
Idealreaktoren fertig sind, einmal eine Frage. Wenn Sie diese Frage beantworten
können, haben Sie im vorliegenden Kurs schon einiges gelernt. Es gibt einen Fall, wo man bei einem Reaktor das Spektrum
experimentell ermitteln kann, ohne einen Dirac-Puls als Aufgabefunktion
anwenden zu müssen, welcher Reaktor und welches Prozedere sind
das? Antwort und zugleich
Erfolgskontrolle !
Schließlich noch eine Frage an Leser, die sich etwas in
Regelungstechnik auskennen (um ihr Gespür für die Verwandtschaft von
Sprungantwortmethode und Summenkurve der Verweilzeit zu 'wecken'):
Welche Streckentypen in der Regelungstechnik
entsprechen dem KIK und dem IR ?
Antwort
Ich weiß nicht, ob es Ihnen nicht auch so geht wie mir: da habe
ich mir das ganze theoretische Zeug einverleibt und frage mich: zu was? Was
kann man damit anfangen? Und weil das gerade an dieser Stelle recht schön
zu machen ist, möchte ich Ihnen mal kurz umreißen, zuwas das
Dargelegte taugt. Sie können nämlich sehr schön aus dem
Verweilzeitspektrum eines realen Reaktors, sein nichtideales Verhalten erkennen
und klassifizieren. Sie können dann mithilfe dieser Informationen recht
gute mathematische Modelle für die Berechnung des Reaktors entwickeln, -
selbst, wenn Sie dazu noch nicht imstande sind, können Sie aber wenigstens
erahnen, daß es so gehen könnte.
8.2.1.) Reale Strömungsrohr-Reaktoren
Welche nichtidealen Ausbildungen des Strömungsmusters in
Rohrreaktoren gibt es?
8.2.1.a.) Randeffekt mit 'Kehrwasserzonen'
Selbst, wenn Sie nicht Kanufahrer sind, haben Sie diesen Effekt schon an
Fluß-/Bach-Ufern gesehen. Der Effekt ist oft so stark, daß echte
Fluß-Aufwärts-Strömungen zu beobachten sind !!
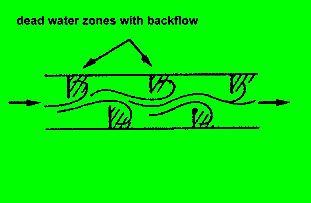
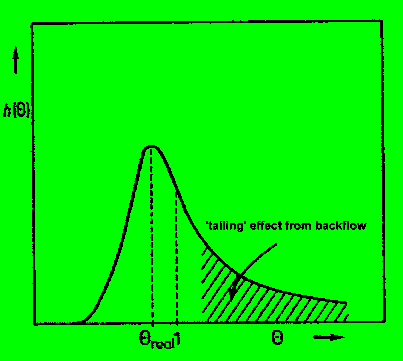
Wie äußert sich das im Spektrum? Vorhersage: wir werden eine
Art 'längere Schwanzbildung' (Tailing) in der spektralen Glockenkurve
beobachten.
Etwa so:
8.2.1.b.) Axiale Dispersion
Wir habe diesen Effekt schon weiter oben erwähnt. Dadurch,
daß in der Rohrströmung eben nicht 'ideale differentielle Scheibchen
forwärtslaufen', sondern Volumenelemente zurückbleiben oder
vorauseilen, z.B. durch Diffusionsprozesse, ergibt sich eine axiale 'Streuung'
(axiale Dispersion). Dieser Effekt kann auch mit einem mathematischen Ansatz
für eine axiale Diffusion modelliert werden (Bodenstein-Modell,
Bodenstein-Zahl). Wenn Sie mit den Formeln nichts anfangen können,
vergessen Sie diese zunächst. Sehen Sie sich nur das Bildchen an
!!
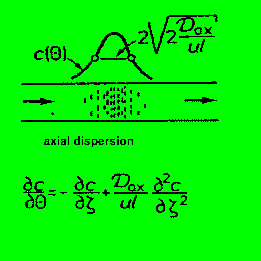
Die axiale Dispersion führt, wie bereits oben erwähnt, zu
einer Verbreiterung der spektralen Nadel (für's IR !!) zu einer
Gauss'schen Glocke. Die Varianz charakterisiert das Ausmaß der axialen
Dispersion.
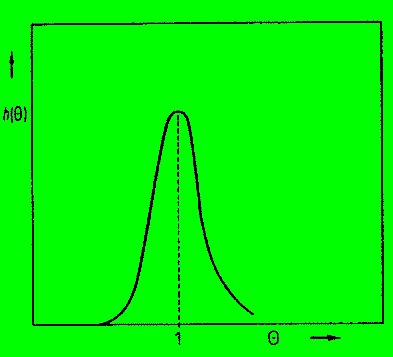
Man könnte sagen, soetwas ist das Mindeste, was man bei realen
Rohren zu erwarten hat.
8.2.1.c.) Effekte in 'gepackten Rohren',
Packungsinhomogenitäten.
Es ist ein offenes Geheimnis, daß Rohrreaktoren in der Heterogenen
Katalyse eine große Rolle Spielen. Die Rohrreaktoren sind mit einer
Katalysatorschüttung 'gepackt' und werden von einer fluiden Mischung (Gas
oder Flüssigkeit) durchströmt (denken Sie im Zweifelsfalle an Ihren
Autokatalysator!!). Wenn die Packung beispielsweise zur Rohrwandung hin etwas
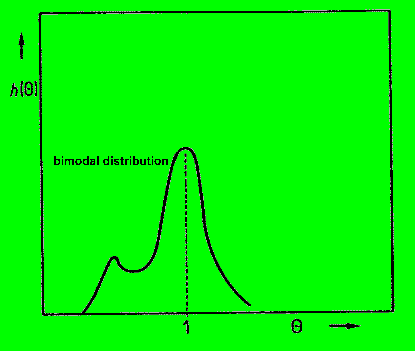
'offener' (lockerer) ausfällt, haben wir den Fall, daß ein Teil der
Fluidmasse viel schneller 'durch ist' als ein anderer, dies wird zu einer
sogenannten Bimodalen Verteilung führen.

dies sieht dann folgendermassen aus:
8.2.2.) Reale Dürchfluß-Rührkessel
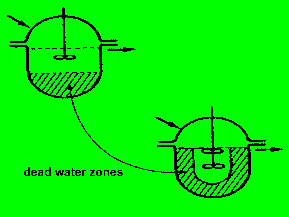
8.2.2.a) Totwasserzonen im Kessel
Wenn das Rührorgan nicht für eine vollständige
Durchmischung des Reaktors sorgen kann, treten 'Totwasser-Bereiche' im Apparat
auf. Beispiele für die rämliche 'Gestalt' dieser Zonen:
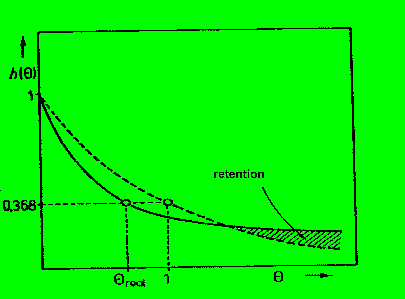
in der nächsten Abbildung zeigt die gestrichelte Linie die
Spektralkurve für den (idealen) KIK und die durchgezogene Linie das reale
Spektrum. Die Totwasserzone führt aufgrund ihres
'Rückhaltevermögens' (Retention) zunächst zu einer relativen
Verzögerung des Traceraustrags, - dieser kommt dann zu den späteren
Zeiten verstärkt 'hinterher'.
8.2.2.b.) Traceradsorption im Kessel
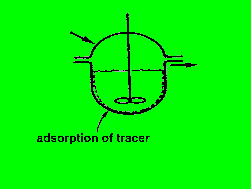
im folgenden Bild ist wieder die gestrichelte Linie für den idealen
Kessel gültig, die durchgezogene für den Realfall.
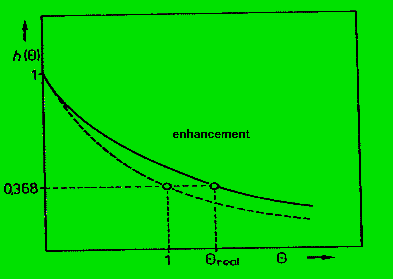
man sieht, daß der an der Kesselwand adsorbierte Tracer zu einer
Verstärkung der Austragsmenge führt, die mit längerer Zeit
zunimmt.
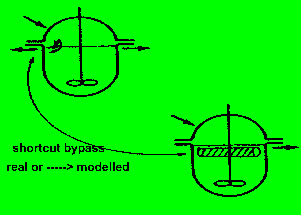
8.2.2.c.) Bypass im Kessel
es ist nicht von der Hand zu weisen, daß in Rührkesseln ein
'Kurzschluß' vom Einlauf zum Auslauf auftritt. Solch ein Kurzschluß
kann in grober Näherung mit einem Rohrbypass modelliert werden
(vorstellungsmäßig und mathematisch), das Bypass-Rohr wird
natürlich wenig ideal sein, also zumindest viel axiale Dispersion
aufweisen.
im folgenden Bild ist wieder die gestrichelte Linie für den idealen
Kessel gültig, die durchgezogene für den Realfall.
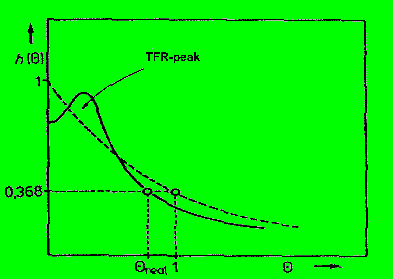
man sieht in der Abbildung, wie die Gauss-Glocke für den
'Rohrbypass' auf die Abklingkurve des Kessels 'aufgehöckert' ist. Fazit:
wenn die Abklingkurve des Rührkessels Höcker oder Sprünge
aufweist, muß an Bypässe gedacht werden. Vielleicht gelingt es in
solchen Fällen dann als allererstes apparative Verbesserungen vorzunehmen.
Sonst muß an eine Modelliereung mit einer Parallelschaltung von
Rührkessel und Rohr gedacht werden.
|
Die
Verweilzeitspektren zeigen bei realen Reaktoren die 'Unregelmässigkeiten'
in der Qualität der Makrovermischung. Die zu beobachtenden Verläufe
bieten Hinweise zu Möglichkeiten einer mathematischen Modellierung dieser
Reaktoren. |
|
Es soll im folgenden nur die chemisch-reaktionstechnische und nicht die
apparativ-technische Optimierung betrachtet werden.
Vorab muß ich Ihnen hier noch eine 'elegante'
Reaktorberechnungsmethode vermitteln und jetzt bin ich endgültig am Ende
mit dem Festhalten an 'formelfrei' !! Versuchen wir wenigstens, die Sache auf
ein Minimum zu reduzieren ! Es handelt sich dabei um die - wenn man sie intus
hat - nutzerfreundliche und anschauliche 1/r(U) - Methode zur
Raumzeitberechnung.
Die 1/r(U)-Methode
Bei einer reaktionstechnischen Optimierung ist man bestrebt, durch
möglichst kurze Zeiten und möglichst kleine Reaktorvolumina eine
möglichst große spezifische Produktleistung zu erreichen. Die
Reaktionsdauer im Reaktor bei gegebenem Reaktorvolumen wird mit dem Begriff
'Raumzeit' (engl. space time) bezeichnet. Als Zusammenhang gilt: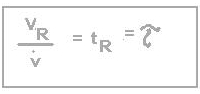
(VR=Reaktorvolumen, tR=Raumzeit,
v-Punkt=Volumenstrom, tau=hydrodynam. Verweilzeit)
Für ideale kontinuierliche Reaktoren ist die Raumzeit gleich der
hydrodynamischen Verweilzeit tau.
Die genannten Größen sind in der Stoffstrombilanz für
den Reaktor (inklusive darin stattfindender Reaktion) enthalten, - das ist ja
auch irgendwie plausibel, denn die Konzentration eines betrachteten Edukts
beispielsweise wird ja einerseits durch die Reaktion und andererseits durch den
Stoffstrom ('Austrag') 'heruntergezogen'. Ein 'kleines Manko' stellt bei der
ganzen mathematischen Betrachtung der zeitlichen und örtlichen
Konzentrationsprofile die Tatsache dar, daß die Verläufe und Pegel
bei unterschiedlichen Ausgangskonzentrationen ganz 'unterschiedlich ausfallen'.
Gebe es da nicht eine Möglichkeit, die 'Sache' - also letztlich den
Reaktionsfortschritt - irgendwie zu normieren? Das ist eigentlich gar nicht so
schwierig, wir brauchen nur die aktuellen Konzentrationswerte (relativ zur
Ausgangskonzentration) durch den Umsatz ausdrücken. Das geht über die
Umsatzdefinition. Aus ihr folgt: c = co(1-U). Löst man die
Stoffstrombilanzen für die idealen Grundreaktortypen unter Verwendung
dieser Beziehung, erhält man folgende Ergebnisse für die Raumzeit
tR:
| Reaktortyp |
Formel (folgt aus
Stoffbilanz!!) |
| nicht rückvermischt: IR,
AIK |
tR = cA,0 * ∫
(dU/-r(U))
/von 0 bis Ux/ |
| voll rückvermischt: KIK |
tR = cA,0 *
U/-r(U)) mit U = Ux |
|
Legende: tR = Raumzeit, U = Umsatz (von
Edukt A als Referenz-Komponente), cA,0 = Anfangskonzentration von
Edukt A, r = Reaktionsgeschwindigkeit, oder besser rA =
Reaktionsgeschwindigkeit, Edukt A betreffend.
Merke: mit tR = VR / v_punkt
kann man auch das Reaktorvolumen berechnen !! (v_punkt =
Strömungsgeschwindigkeit, z. B. in m3/h ) |
Wenn Sie Ihr Wissen später anhand der vertiefenden Fachliteratur
ergänzen, werden Sie dort auch die Herleitung der Formeln finden.
Wenn Sie das schon mal ansehen wollen, dann bitte hier:
Wenn wir diese Formeln genauer ansehen, bemerken wir, daß die
Raumzeit proportional zum Produkt aus U und 1/r(U) ist. Dies bedeutet also
nichts anderes, als daß das Integral unter der Fläche der Kurve
1/r(U) = f(U) in den Grenzen von Uo bis Ux der Wert der Raumzeit
ist.
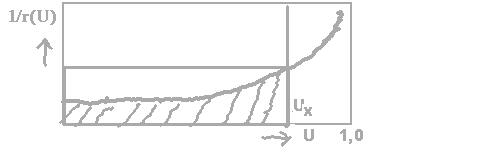
Für nicht raumzeitstationäre Reaktoren ist die Raumzeit
gegeben durch die Fläche unter der Kurve 1/r(U) = f(U). Für den
raumzeitstationären kontinuierlichen Durchflußrührkessel
dagagen ist über den ganzen Reaktionsraum der gleiche Konzentrationswert
und damit auch Umsatzwert - aber ebenso auch 1/r(U)-Wert - vorhanden, die
Raumzeit entspricht deshalb in diesem Fall der Rechteckfläche U*1/r(U).
Das alles ist eine direkte Konsequenz der obenaufgeführten beiden Formeln
und eigentlich auch plausibel.
Und schon können wir mit dieser 'Darstellungsmethode' eine klare
Regel ganz augenfällig veranschaulichen, nämlich:
Bei einfachen bzw. eindeutigen Reaktionen, bei denen der
Reaktionsfortschritt und die Produktbildung alleine mit dem Umsatz
verknüpft ist, ist die Raumzeit in den nicht raumzeitstationären
Reaktoren AIK und IR immer kleiner als im raumzeitstationären KIK. Man
spricht hier von einer umsatzorientierten Reaktoroptimierung. Ein Kriterium
für diese Eigenschaft der 'eindeutigen Umsatzabhängigkeit' ist -
allerdings mit Einschränkungen - der Kurvenverlauf in der obigen
Darstellung. Man sieht z.B. auch aus obiger Kurve, daß wenn die Kurve
sich assymptotisch an U = 1,0 nähert, auf jeden Fall (unabhängig vom
Reaktortyp) unendliche Raumzeiten erforderlich sind, - so etwas liegt z:.B. vor
allem auch bei Gleichgewichtsreaktionen vor (hier sogar nicht nur mit U = 1,0
als Assymptote, sondern beim Gleichgewichtsumsatz). Ebenso könnten
Reaktionen mit Verläufen, die zum Ursprung hin assymptotisch zur Y-Achse
verlaufen, zu anderen Optionen führen, - und dies ist auch der Fall und
soll in kürze besprochen werden.
|
Bei eindeutigen
umsatzorientierten Reaktionen ist die Raumzeit und damit die spezifische
Produktleistung in den nicht raumzeitstationären Reaktortypen immer
optimaler als im raumzeitstationären KIK. |
|
Gibt es aber eventuell die Möglichkeit, mit Hilfe von
Reaktorschaltungen - hier natürlich vor allem einmal mit
Kaskaden - die 'schlechte' Produktleistung des
Durchflußrührkessels zu verbessern ? Nehmen wir als Beispiel eine
Kaskade von 3 etwa gleichgroßen Kesseln, für die das nachfolgende
Bild zutreffend wäre. Wenn wir unseren gewünschten Gesamtumsatz
über die 3 Kessel mit passenden Teilumsätzen 'verteilen', ist die
Raumzeit für diese Kaskade die Addition der 3 Rechteckflächen
ΔU*1/r(U). In der folgenden Abbildung ist die schraffierte Fläche a
- bekanntermassen - die Raumzeit in einem AIK oder IR. Die Fläche a+b
wäre - ebenfalls bekanntermassen - die Raumzeit im KIK. Die Fläche
unter der 3- stufigen 'Staffel' (Fläche a+die 3 Treppenstufen über
der Kurve) entspricht der Raumzeit in unserer Kaskade.
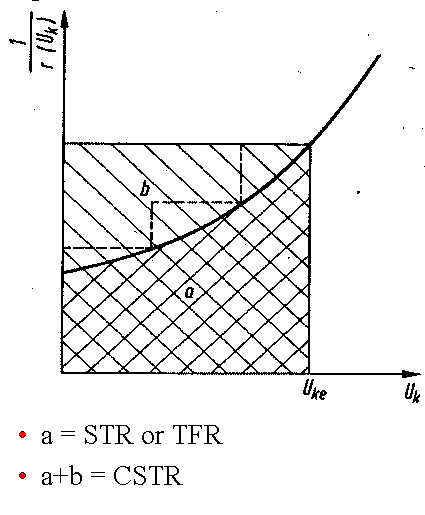
wir sehen aus der Abbildung, daß für eine Kaskade mit
nur 3 Kesseln schon eine wirklich dramatische Verbesserung in der
Raumzeit gegenüber dem KIK erhalten wird (Sie können die Flächen
ja mal prozentual abschätzen !!), obwohl diese Reaktoranordnung vom
Rückvermischungsmuster her noch lange nicht als 'ideal
nicht-rückvermischt' angesehen werden kann !!!
Hiermit haben wir ein früher schon getroffenes
Statement belegt.
Ich glaube, Sie sehen hiermit schon sehr gut, wie nützlich die
1/r(U)-Methode ist. Weitere Beispiele finden Sie in den Übungen des Buchs
/6/ von J. Hagen (siehe Literatur).
Im Grunde genommen war das vorherige Beispiel formal auch schon eine
Anwendung mit Konzentrationsführung, - ja man könnte sogar soweit
verallgemeinern, daß jede Reaktionsdurchführung in einem
Reaktionsapparat eine Konzentrationsführung darstellt. Im vorliegenden
soll die Konzentrationsführung jedoch im etwas engeren Sinn, d.h. vor
allem aus der Notwendigkeit der Eigenheiten der Reaktion heraus folgend und im
Falle der 'Nichtdurchführbarkeit' einer umsatzorientierten Optimierung,
erörtert werden.
Bei komplexeren Reaktionsnetzwerken, beginnend mit
einfachen Gleichgewichtsreaktionen über Parallel- und Folgereaktionen bis
hin zu offenen und geschlossenen (Gesamt-)Folgereaktionen konnten wir ja schon
zeigen, daß für bestimmte Produktbildungsgeschwindigkeiten bestimmte
Komponentenkonzentrationen optimal (z.B. maximal) 'eingestellt' werden
müssen.
| Die umsatzorientierte Reaktor-Optimierung
ist im Grunde genommen ein einfacher Spezialfall der Optimierung durch eine
geeignete Konzentrationsführung. |
Betrachtet man bei einfachen Folgereaktionen die 1/r(U)
- Funktion für den Eduktverbrauch, so scheint hier keines der genannten
Probleme aufzutreten und man könnte an eine rein umsatzorientierte
Optimierung denken. Aber dem ist nicht so !! Lassen Sie uns das erarbeiten
!
betrachten wir : eine einfache Folgereaktion A
-> B -> C mit irreversiblen Teilschritten und den
Geschwindigkeitskonstanten k1 und k2, - nehmen wir noch
zusätzlich für beide Teilschritte eine Reaktionsordnung von 1 an
!
das
Folgende ist alles großenteils Wiederholung !!!
von oben kennen Sie die kinetischen Gleichungen:
dcA/dt = -k1 cA
dcB/dt =
k1cA - k2cB
dcC/dt =
k2cB
die Konzentrations-Veraufskurven für A,B und C
hängen vom Verhältnis k1/k2 ab, Sie erinnern
sich an die Abbildungen !
Wir können aus den Kurven entnehmen, daß die
Konzentration des Produkts B ein Maximum annimmt, wenn k1 >
k2 ist, oder zumindest nah bei k1 = k2 liegt.
Und wir realisieren auch, daß keine ausreichenden
Mengen an B erhalten können, wenn umgekehrt k2 >>
k1 ist. In diesem Fall gelingt es uns kaum, mit reaktionstechnischen
Mitteln B zu produzieren. Wir müssen hier etwas an unserer 'Chemie'
ändern und beispielsweise einen katalytischen Prozeß ausarbeiten,
der die Bildung von B begünstigt. Oder wir können versuchen,
k1/k2 durch die Wahl einer geigneten Reaktionstemperatur
zu beeinflußen.
lassen Sie uns nun zusammenstellen: was
müssen wir tun, wenn::
C unser gewünschtes Produkt ist
? ----> das ist der einfachste Fall: wir brauchen nur einen
möglichst hohen Umsatz von A anstreben und damit verbunden eine relativ
lange Reaktionsdauer. Wir befinden uns hier im Regime der umsatzorientierten
Optimierung. Wenn k2 >> k1 ist, sollten wir keine
kleinen Umsatzwerte auswählen ! (klar ? )
B unser
gewünschtes Produkt ist ? -----> für k1 >>
k2 haben wir eine gute Chance, eine ausreichende Menge an
Zwischenprodukt B zu erhalten. Aber wir dürfen keinen (beliebig) hohen
Umsatz wählen, wozu man ja geneigt wäre, wenn man nur auf den 1/r(U)
- Kurvenverlauf des Eduktverbrauchs achten würde. Ja wir sehen sogar,
daß B ein Maximum Bmax annimmt bei einer speziellen
Reaktionsdauer taumax. Das bedeutet, daß wir ein Maximum an B
erhalten werden, wenn wir unsere Reaktion derart 'betreiben', daß alle
Reaktanden exakt für die Dauer taumax 'zusammenbleiben'.
Für den absatzweisen Betrieb (also im AIK) können wir eine Formel
für Bmax und taumax herleiten (normale
Reaktionskinetik = absatzweise Kinetik !!), - hierzu gibt es Übungen in
der Literatur. Auf der anderen Seite wissen Sie ja, daß man die Daten
für ein IR aus denen für den AIK durch 'Zeit-Ort-Transformation'
herleiten kann ! (klar?). Schließlich kann man natürlich auch
für den vollständig rückvermischten KIK aus der Stoffbilanz
einen Zusammenhang zwischen Bmax und taumax herleiten (
siehe z.B. bei J. Hagen /6/ ).
Wenn man nun die erhaltenen Ergebnisse für
Bmax und taumax für vorgegebene Reaktionsdaten
für einen AIK und ein IR einerseits und für den KIK andererseits
vergleicht, dann sehen wir (fast schon erwartungsgemäß !!),
daß taumax kürzer und Bmax höher ist
für AIK und IR - im Vergleich zum KIK.
wenn B das
gewünschte Produkt ist und k1 > k2, erhalten wir
ein Maximum an B in einem nicht rückvermischten Reaktor, d.h. AIK oder IR,
wenn wir den Reaktor bei taumax (und damit auch Umax)
betreiben.
Dieses Ergebnis können wir uns einerseits aus
der Verweilzeitinformation, d.h. der Makrovermischungscharakteristik, oder aber
andererseits auch rein formal aus der 1/r(U)-
Methode heraus plausibel machen.
In den nicht rückvermischten
Reaktoren ist die Verweilzeit der Reaktanden exakt gleich der hydrodynamischen
Verweilzeit, im vollständig rückvermischten Reaktor haben wir eine
spektrale Verteilungskurve in Form einer e-Funktion, - damit existieren 'auch'
Reaktanden-Verweildauern, die nicht optimal sind.
Bei der
1/r(U)-Methode haben wir verlaufsmässig das gleiche Bild für
den Edukt-Umsatz, wie bei der einfachen umsatzorientierten Optimierung, -
lediglich, daß hier nur vom Umsatz 0 bis zum Umsatz Umax
'gefahren' werden darf. Im KIK wäre dann die Raumzeit wieder die
Rechteckfläche 1/r(Umax) * Umax und für AIK und
IR die Fläche unter der Kurve 1/r(U) = f(U) von U = 0 bis Umax
(ist das klar ?). .
Etwas salopp formuliert, könnte man sagen:
Der
Funktionsverlauf von 1/r(U) charakterisiert das (im Vorliegenden vielzitierte)
Wesen der Reaktion (Reaktionseigenschaften).
Das
Ergebnis der Flächenauswertung im 1/r(U)-Graphen ist eine Folge der
implementierten Art der Rückvermischung (Reaktoreigenschaft) |
Zur Fortsetzung habe ich mich für ein 'neues Verfahren'
entschieden:
ich übernehme im folgenden zunächst teilweise den
englischen Text aus meinen online-Kursen, die ich schon früher verfasst
habe und übersetze und adaptiere diese peu a peu. Der Leser kann sich dann
schon etwas vorwärts arbeiten und sieht auch, was alles noch geplant ist.
'A wing English' (ein wenig Englisch) schadet Ihnen auch nichts. |
So, wie es eine Datumsgrenze gibt, gibt es ab jetzt bei mir im
vorliegenden online-Kurs eine Übersetzungsgrenze. Diese soll so
aussehen:
 --------
Beginn: 11.03.06
--------
Beginn: 11.03.06
bis zu dieser Grenze ist im folgenden alles in Deutsch übersetzt.
Der Leser hat so gleichzeitig mal die Kontrolle, wie fleißig oder faul
der Autor ist !!
Wie bereits erwähnt, ist die einfache Gleichgewichtsreaktion A
<-> B kinetisch gesehen einer Folgereaktion sehr ähnlich. Mann
könnte sie nämlich formal als Sonderfall der Folgereaktion A -> B
-> A auffasssen. Es ist also zu erwarten, daß die Ergebnisse einer
Betrachtung nicht dramatisch verschieden von denen der Folgereaktion sind.
die einfache reversible Reaktion A <-> B mit
den Geschwindigkeitskonstanten erster Ordnung k1 (Hinreaktion) und
k2 (Rückreaktion):
Wenn wir mit cB,0 = 0 starten, wird die
Reaktion Produkt B erzeugen, bis der Maximalumsatz UA,max erreicht
wird. Dieser Maximale Umsatz wird durch die Thermodynamische
Gleichgewichtskonstante K = k2/k1 bestimmt. Für die
Berechnung des Maximalen Umsatzes setzt man zuerst die kinetische Gleichung
an:
rA = -dcA/dt = k1 cA -
k2 cB
im nächsten Schritt ersetzt man die
Konzentrationen durch den Umsatz UA:
cA =
cA,0(1-UA)
cB =
cB,0UA
aus der Geschwindigkeitsgleichung
erhält man:
dUA/dt = k1(1-UA) -
k2UA
im Gleichgewicht gilt dann
für
UA,max: dUA/dt = 0
hieraus
folgt:
UA,max =
k1/(k1+k2)
dies ist der Maximale Umsatz
einer reversiblen Reaktion .
Welche Konsequenz hat dies für die
Raumzeit-Optimierung ?
Es ist augenfällig, daß wir diese
Reaktion mit der umsatzorientierten Methode behandeln können, aber wir
müssen - was sehr wichtig ist - darauf achten, daß UA,max
als höchstmöglicher Umsatz nicht überschritten wird, - denn
'mehr genehmigt uns die Reaktion einfach nicht' !! Formal können wir
dieses Vorgehen als Optimierung mit Konzentrationsführung im engeren Sinne
bezeichnen, aber das ist - wie gesagt - ein wenig Definitionssache. Inzwischen
wissen wir ja auch, daß wir den nicht-rückvermischten Reaktortyp
für den vorliegenden Fall wählen müssen.
Eine
interessante Frage ist - und das ist eine typische Übungsaufgabe in der
Technischen Chemie - wie lange es dauert, bis die reversible Reaktion ihr
Gleichgewicht erreicht hat, oder genauer gesagt zu z.B. 90%, 95% oder 99%
erreicht hat, - (warum ? und läßt sich das auch formal zeigen?
)
|
Fazit für die beiden obenerwähnten Reaktionstypen (Folge
und Gleichgewicht):
beide Reaktionen zeigen das typische Verhalten,
daß man bei alleiniger Betrachtung der 1/r(U) - Kurven - die ja für
den Edukt-Verbrauch gelten - meinen könnte, sie könnten einfach
umsatzorientiert optimiert werden. In Wirklichkeit haben wir aber in unseren
obigen Betrachtungen bemerkt, daß man die Reaktionen nicht bis zu einem
beliebig hohen Umsatz fortschreiten lassen kann und darf. Wir können die
Reaktion nur bis zu einem maximalen = optimalen Umsatz fahren. Das bedeutet
aber wiederum, daß wir die Reaktionsdauer exakt einhalten müssen und
wir wissen ja jetzt schon, daß dies in einem nicht-rückvermischten
Reaktor (also AIK oder IR) funktioniert. Im Grunde genommen können wir das
Ganze auch so formulieren: bei diesen Reaktionen können wir ebenfalls
umsatzorientiert optimieren, - nur daß wir einen 'Grenzumsatz' nicht
überschreiten dürfen. |
Parallel reactions
Parallelreaktionen verhalten sich grundsätzlich
ähnlich wie die obigen Grundreaktions-Typen. Nehmen wir als Beispiel
wieder einen einfachen Fall: A - >B parallel zu A -> C, also eine
irreversible Parallelreaktion. In einer Parallelreaktion laufen die beiden
'Reaktionszweige' konkurrierend ab. Man sieht aus
reaktionskinetischer Sicht, daß das 'Produktionsverhältnis' der zwei
Zweige - dies ist identisch mit dem Verhältnis der
Reaktionsgeschwindigkeiten derselben - von den Geschwindigkeitskonstanten und
den Reaktions-Ordnungen der beiden konkurrierenden Reaktionen abhängt.
Formal läßt sich herleiten (und wir kennen diese Formel bereits):
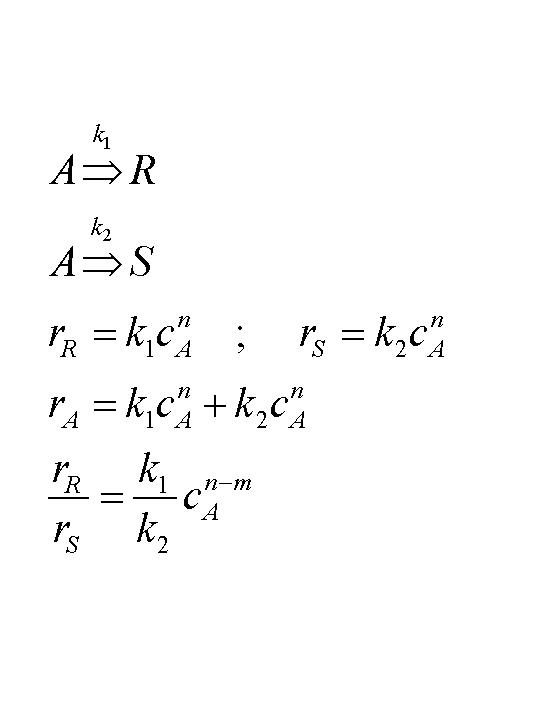
Reaktionskinetik einer einfachen Parallelreaktion
Für zwei Reaktionszweige mit der gleichen
Reaktionsordnung, z.B. mit Ordnung 1, ist mit n=m das Verhältnis der
Reaktionsgeschwindigkeiten identisch mit dem der Geschwindigkeitskonstanten.
Hierfür läßt isch ableiten:
| Grösse |
Formel |
| relative Produkt- konzentration cB/cA,0 |
cB/cA,0 = (
k1/(k1+k2) ) *
UA |
| relative Produkt- konzentration cC/cA,0 |
cC/cA,0 = (
k2/(k1+k2) ) *
UA |
| Selektivität SB |
SB = k1/(k1+k2) |
| Selektivität SC |
SC = k2/(k1+k2) |
| Produktverhältnis cB/cC |
cB/cC = k1/k2 |
für den Fall unterschiedlicher Reaktionsordnungen
sieht man aus der Formel, daß die aktuelle Konzentration von A von
Einfluß ist, - das heißt, daß wir A mithilfe einer
Konzentrationsführung einstellen müssen !!! Nehmen wir einmal an, die
erste Reaktion sei von niedrigerer Ordnung (z.B. 1. Ordnung) als die zweite
(z.B. 2. Ordnung). Dann können wir allgemein festhalten, daß der
Reaktionszweig mit höherer Ordnung begünstigt sein wird, wenn die
'treibende Kraft Edukt-Konzentration' verhältnismässig hoch ist.
Dieser Zweig wird dagegen nicht begünstigt, wenn die Konzentration an A
relativ niedrig ist ( meine Eselsbrücke: 1 mal 1 = 1, aber 0,1 mal 0,1 =
0,01 !!!).
Wir können also festhalten:
- wenn der 'gewünschte Reaktionszweig' von
höherer Ordnung ist, sollten wir Rückvermischung vermeiden, um immer
eine relativ hohe Eduktkonzentration einzustellen. Deshalb fällt die
Reaktorwahl auf ein Strömungsrohr oder eine Kaskade. Im Falle der Kaskade
könnte man sogar 'mit zunehmender Kesselgröße' arbeiten, um
immer 'möglichst wenig Rückvermischung von niedrigem cA'
einzustellen !!
Beispiel einer 'aufsteigenden'
Kaskade
- wenn dagegen der gewünschte Produktbildungszweig
von niedrigerer Ordnung ist, sollten wir (möglichst viel)
Rückvermischung einsetzen, damit wir immer eine relativ niedrige
Eduktkonzentration einstellen. Deshalb ist ein großer kontinuierlicher
Durchflußrührkessel (KIK) 'unser' Reaktor (nicht vergessen: 'rein
und runter' !!). Alternativ wäre in Umkehr zum vorhergehenden Fall eine
Kaskade mit 'absteigender Kesselgröße' denkbar, - oder, wenn aus
irgendeinem Grund ein Rohrreaktor eingesetzt werden soll, - dann müsste
man eine spezielle Reaktorschaltung verwirklichen, bei der im Rohr
cA immer sehr klein gehalten wird, - und deshalb 'auf der Strecke'
immer wieder in geringen Mengen nachdosiert wird. In gleicher Weise könnte
man natürlich auch in einer 'gleichkessligen' Kaskade (als
Rohrannäherung) verfahren.
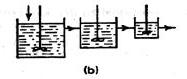
'absteigende'
Kaskade
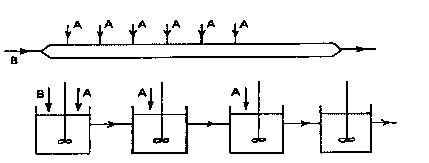
Rohr und
Kaskade mit 'Feedback'
9.2.4.) Exotische Reaktionen ? Autokatalytische
Reaktionen
Autokatalytische Reaktionen speziell sind nicht unbedingt 'grenzenlos
häufig' vorkommende Reaktionen. Wir sehen aber in ihrer Betrachtung vieles
über das 'Wesen' der Konzentrationsführung. Und es gibt im
übrigen doch auch sehr viele Reaktionen, die - schon aus dem Verlauf der
1/r(U)-Kurve heraus erkennbar - komplizierter sind und mit einer einfachen
umsatzorientierten Optimierung nicht behandelt werden können, - gerade
auch im Bereich der Katalytischen und Makromolekularen Reaktionen. Hierfür
steht - didaktisch gesehen - stellvertretend die im folgende beschriebene
Autokatalytische Reaktion.
In Autokatalytischen Reaktionen ist die
Reaktionsgeschwindigkeit proportional zur Konzentration (normalerweise) eines
Produkts (oder oft ganz einfach: des Produkts). Im einfachsten Fall kann das
eine Abhängigkeit von 1. Ordnung sein, also beispielsweise:
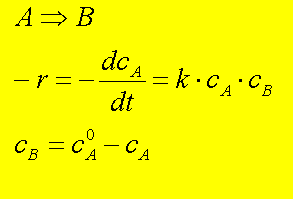
Wenn man CB über CA0 in
CA ausdrückt, sieht man, daß die Abhängigkeit von
rA von cA quadratisch ist und wenn wir rA in
Abhängigkeit von cA auftragen, erhalten wir eine Parabel mit
einem Maximum bei cA = cA,0/2 . Das kann man formal
herleiten:
rA = kcA,0*cA - k
c2A
drA/dcA = 0 =
k(cA,0 - 2 cA) -> cA = cA,0/2
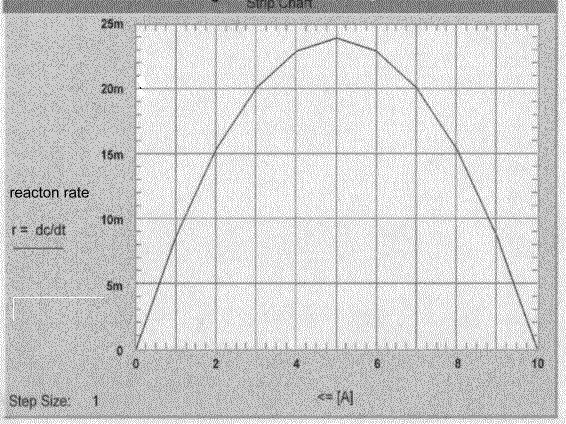
Autokatalytische Reaktion, parabolische Funktion
Wir sehen also, daß die Reaktionsgeschwindigkeit
ein Maximum bei 50 % Umsatz annimmt. Und wir 'entdecken', daß wenn die
Produktkonzentration exakt Null ist, die Reaktionsgeschwindigkeit ebenfalls
Null ist. Das bedeutet aber, daß die Reaktion nicht stattfindet, wenn die
Produktkonzentration Null ist ( das riecht ja förmlich nach der
Notwendigkeit einer Rückvermischung). Wenn man die Parabelfunktion
rA = f(cA) in die Form 1/rA(UA) =
f(UA) bringt, erhält man wieder eine Parabelfunktion. Diese ist
jedoch 'nach oben geöffnet' und zeigt ein Minimum bei U = 50%.
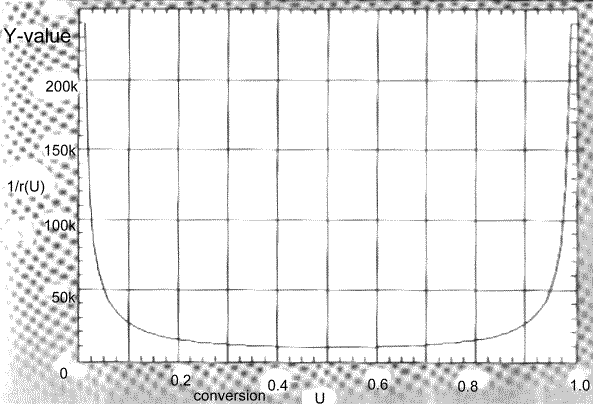
der
1/r(U) - Plot
Was sehen wir daraus ?
- die Funktion 1/r(U) = f(U) steigt nicht stetig
für U=0 bis 1, sie hat ein Minimum bei 50 % Umsatz und hat vor allem bei
U=0 eine Unstetigkeitsstelle (neben der bei chemischen Reaktionen üblichen
Stelle U=1).
- wenn wir versuchen, von U = 0 bis x (z.B. U = 0.8)
die Funktion zu integrieren, wird die Fläche und damit die Raumzeit
unendlich groß, - was ja der Raumzeit in den nicht-rückvermischten
Reaktoren entspricht . Das ist plausibel, denn bei Umsatz Null ist die Reaktion
'abgestoppt', oder besser: 'sie kommt da nicht zu Gange!!' (Realisieren Sie
auch, daß r = 0 ---> 1/r = ∞zur Folge hat !!)
- man sieht auch schön, daß die
Rechteckfläche, die man für den vollständig rückvermischten
KIK im Bereich U = 0 bis U = 50% 'aufziehen' kann, bei weitem die kleinste im
ganzen Graphen erhältliche Fläche darstellt, was mit anderen Worten
bedeutet, daß für 50% Umsatz der KIK die höchste spezifische
Produktleistung bietet. Aber auch für Umsätze unter 50% ist der KIK
der beste Reaktor, weil in allen Fällen die Rechteckfläche des KIKs
kleiner ist, als die Flächenintegrale unter der Funktionskurve. Es bringt
also nicht so viel, einen nicht-rückvermischten Reaktor mit einer geringen
Produktmenge 'anzuimpfen', wie es vergleichsweise der Einsatz des KIK mit sich
bringt.
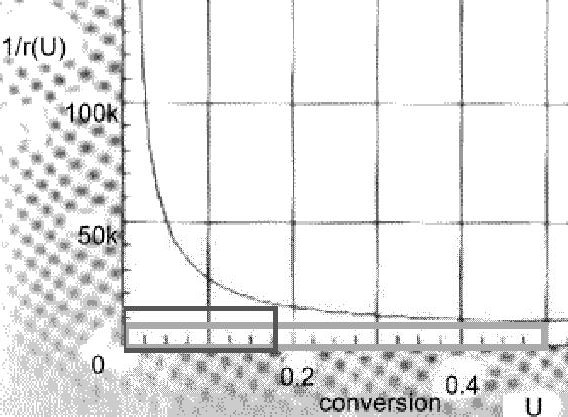
vergrößerter 1/r(U)-plot, - 'graues' Rechteck =
KIK mit 50% Umsatz,
'schwarzes' Rechteck = beliebiger Umsatz unter 50% (im
KIK) l
- wie gesagt, für die rückvermischten
Reaktoren gilt, daß wir überhaupt nicht mit U = 0 starten
können, wir benötigen eine 'Initialisierungs-Menge' an Produkt, um
von der Unstetigkeitsstelle U = 0 wegzukommen.
- da der Funktionsverlauf oberhalb von U = 50 %
'normal' ist, können wir erwarten, daß wir in diesem Bereich im
Regime der üblichen Umsatzorientierten Optimierung sind. Das hat zur
Folge, daß wir mit einer Reaktorserienschaltung von KIK ( für U = 0
bis 0,5) und einem Strömumgsrohr für den restlichen Bereich die
effizienteste Konzentrationsführung erreichen müssten.
Da wir ja
auch wissen, daß der KIK im umsatzorientierten Bereich der Verlierer ist,
werden wir es vermeiden, an einen Umsatz oberhalb 50% im KIK auch nur zu
denken. Das könnten Sie sich schön mit einer selbstgefertigten Skizze
mal vor Augen halten. Ausserdem können Sie sich in der Tabelle unten, gut
davon überzeugen.
- ein Kreislaufreaktor mit optimal eingstelltem
Kreislauffaktor könnte bei unserem Problem noch ein alternativer
Kompromiss zur erwähnten Serienschaltung sein. Näheres über die
Behandlung von Kreislaufreaktoren - vor allem mit der 1/r(U) - Methode findet
sich bei Hagen /6/ . Es empfiehlt sich wirklich sehr, dort
nachzusehen.
- Ein weiterer Kompromiss wäre eine Kaskade mit
ab U = 50 % kleiner werdenden Kesseln, ähnlich wie sie oben bereits
aufgezeigt wurde.
Lassen Sie uns nun das Behauptete mit Daten aus einer
Übung der Techn.Chemie - sozusagen zweifelsfrei -
belegen:
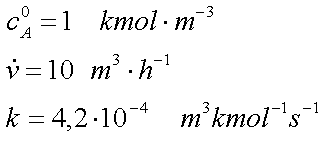
Beispiel einer Autokatalytischen Reaktion
Aufgabenstellung der Übung war: welcher
Reaktor oder welche Reaktorschaltung weist die niedrigste Raumzeit für die
o.a. Reaktion auf, wenn ein Umsatz von 99% erzielt werden soll ?
Was war
zu machen ? Es mussten die Raumzeiten nach der 1/r(U) - Methode für
verschiedene Reaktoranordnungen berechnet werden, - eine typische Rechenaufgabe
der Technischen Chemie. "You should try it".
| Eine etwas 'abstrakte' Anmerkung muss hier noch erwähnt
werden: die Autokatalytische Reaktion läuft streng nach ihrer Kinetik
betrachtet ohne eine - wenn auch nur winzigste - Spur von Produkt B gar nicht
an !!! Das hat aber für den KIK die etwas 'irre' anmutende Konsequenz,
dass die Reaktion beim Anfahren des KIK gar nicht anläuft !!! Es muss
deshalb ganz deutlich festgehalten werden, dass bei allen Betrachtungen im
vorliegenden Text vom eingefahrenen = stationären Betrieb der Reaktoren
ausgegangen wird. In diesem Fall ist im KIK ja schon die maximale Konzentration
an Produkt B erreicht !! (In der Anfahrphase müsste also mit B 'angeimpft'
werden) |
hier nun die Ergebnisse :
für 99 % Umsatz und die gegebenen Werte erhält man für
die kontinuierlichen Reaktoren (KIK,IR):
| Reaktor oder Reaktorschaltung |
Reaktorvolumen |
| KIK 99 % Umsatz (vergleiche hierzu KIK mit 50% Umsatz s.u.) |
661.4 m3 |
| IR 99 % Umsatz mit cB,0 = 0.000 mol/l |
unendlich |
| IR 99 % Umsatz mit cB,0 = 0.01 mol/l |
60.78 m3 |
| IR 99 % Umsatz mit cB,0 = 0.0001 mol/l |
76.06 m3 |
| IR 99 % Umsatz mit cB,0 = 0.00001 mol/l |
106.5 m3 |
Serienschaltung:
KIK mit 50 % Umsatz VR = 13.23
m3
+
IR für den Rest von 49% (auf 99%) VR =
30.39 m3 |
43.62 m3 |
| Kreislaufreaktor mit optimalem Kreislauffaktor R = 0.188 |
49,47 m3 |
Sie erinnern sich hoffentlich, daß Raumzeit und Reaktorvolumen
über die Strömungsgeschwindigkeit (Volumenstrom) zusammenhängen.
Ein kleines Reaktorvolumen ist gleichbedeutend mit einer kurzen Raumzeit - und
damit einer großen Spezifischen Produktleistung. Dies ist wichtig, wenn
man den Absatzweisen Rührkessel AIK mit in Betracht ziehen will. Dieser
erbringt ja bei der 1/r(U) -Methode die gleiche Raumzeit wie das IR.
Man sieht schön, daß wie prognostiziert, die
Serienschaltung der 'Sieger' ist, gefolgt vom Kreislaufreaktor. Der Unterschied
zwischen der Reaktorschaltung und einem KIK mit 99% Umsatz ist gewaltig.
Für das Animpfen von IRs wird für kleinere Reaktorvolumina schon eine
ansehliche Menge Produkt benötigt.
ein weiteres interssantes
Beispiel für Reaktionen, die eine anfängliche Rückvermischung
erfordern, gibt es im Themenbereich Wärmehaushalt von Reaktoren. Es
handelt sich, wie man sich fast denken kann, um Reaktionen, die zum Start eine
Wärmezufuhr benötigen. Hierbei spielt die Lösung der
verkoppelten Stoff- und Wärmebilanz eine
Rolle.
*****************************************
das signifikante Merkmal der besprochenen Reaktionen
ist, daß sie unerlässlich auf eine anfängliche
Rückvermischung angewiesen sind, weil sie aus reaktionskinetischen (und
thermischen) Gründen anders gar nicht starten könnten. Derartige
Reaktionen trifft man in der Praxis schon häfiger an.
|
Bei der reaktionstechnischen Optimierung durch
Konzentrationsführung werden durch die Wahl geeigneter Reaktortypen oder
Reaktorschaltungen Konzentrationen von Komponenten, die von Einfluß sind,
derart eingestellt, daß ein Optimum an Reaktionsgeschwindigkeit für
die Produktbildung erreicht wird. Die 1/r(U) - Methode ist dabei hilfreich,
kann aber nicht immer alleine zur Auswahl herangezogen werden, weil sie
eigentlich nur das von der Eduktumsetzung herkommende Bild berücksichtigt.
Eine eingehende Analyse des Reaktions-Netzwerks und der Reaktionskinetik ist
erforderlich. |
|
|
|
und so geht's weiter in Teil
4 :
9.3.) Heterogene Reaktionen, - Stoffstromführung
9.4.) Reale Reaktoren, die 'Flächenmethode'
10.) Der Wärmehaushalt von Reaktoren |
pdf-Datei des vorliegenden
Teils 3 (ca. 700k), Feb. 2009
zurück zu Teil 1
zurück zu Teil 2
weiter zu Teil 4
Bitte teilen Sie mir mit, wenn ein Interesse am vorliegenden Stoff
besteht ! Ganz toll wäre auch, wenn ich auf Fehler aufmerksam gemacht
würde.
zur
Homepage des Autors
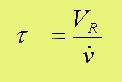 mit:
mit: