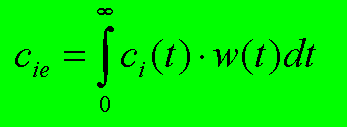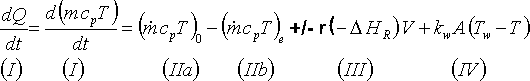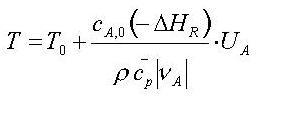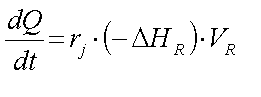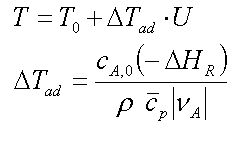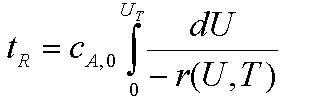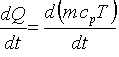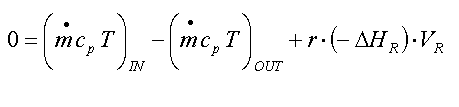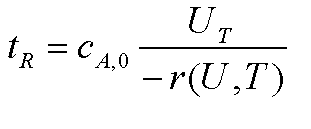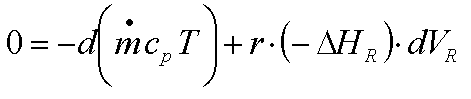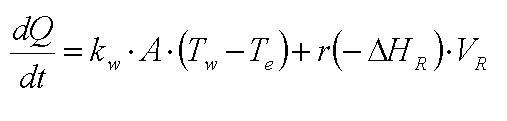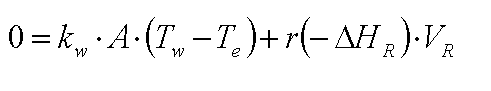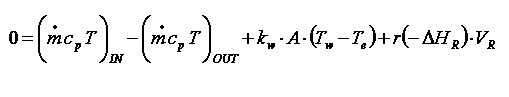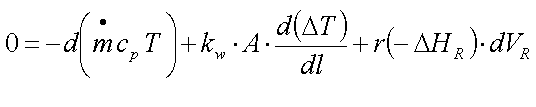Fortbildung für technisch interessierte Laien: 'Was ist chemische
Reaktionstechnik?' - Teil 4
zurück zu Teil 1
zurück zu Teil 2
zurück zu Teil 3
zur
Homepage des Autors
9.3.) Heterogene Reaktionen, - Stoffstromführung (Kurzinfo)
Die Begriffe Stoffstromführung und
Konzentrationsführung können leicht verwechselt werden.
Am einfachsten fällt die Unterscheidung, wenn man sich merkt:
"Konzentrationsführung in homogenen, bzw. pseudohomogenen Systemen
mit 'Charakteristikum Bulk Reaktion' (Lösungen, Emulsionen, Suspensionen
etc., - wobei 'alles reagiert')" ; "Stoffstromführung in
heterogenen Sytemen mit 'Charakteristikum Grenzflächenreaktion' (Fluid
wird an festem Katalysator vorbeigeführt (Oberflächenreaktion),
Fluid-/Fluid-Reaktionen - z.B. Extraktiv-Reaktionen
-,Gas-/Flüssigkeitsreaktionen an Blasen-, Film- oder
Tropfen-Oberflächen u.v.a.)"
|
Wiederholung:
Bei der
reaktionstechnischen Optimierung durch Konzentrationsführung werden durch
die Wahl geeigneter Reaktortypen oder Reaktorschaltungen Konzentrationen von
Komponenten, die von Einfluß sind, derart eingestellt, daß ein
Optimum an Reaktionsgeschwindigkeit für die Produktbildung erreicht wird.
Die 1/r(U) - Methode ist dabei hilfreich, kann aber nicht alleine zur Auswhl
herangezogen werden, weil sie eigentlich nur das von der Eduktumsetzung
herkommende Bild berücksichtigt. Eine eingehende Analyse des
Reaktions-Netzwerks und der Reaktionskinetik ist
erforderlich. |
|
|
|
Stoffstromführungen
sind weitaus
komplizierter zu behandeln. Man könnte da jedem System eine eigene
Internetseite widmen. In einem gewissen Umfang ist für dieses Gebiet auch
die Kenntnis von Makro- und Mikrokinetik heterogener und heterogenkatalytischer
Reaktionen erforderlich.
Zunächst einmal, was für
Möglichkeiten und Phänomene gibt es ?
Heterogene Stoffströme
können im wesentlichen eine Kontaktierung im Gleichstrom, im Gegenstrom
und im Kreuzstrom beinhalten. Es können Filme, Tropfen und Blasen,
Feststoffoberflächen u.a. in glatter und poröser Form als
Kontaktierungsflächen auftreten.
Es ist für diesen Punkt geplant, einige informative
Beispiele auszusuchen, um wenigstens ein grobes Bild von der Vielfalt dieser
Materie zu vermitteln. |
|
|
Tennisball-Rösten im Gleichstrom
Tennisball-Rösten im Gegenstrom
Tennisball-Rösten im Kreuzstrom
mit freundlicher Genehmigung des Instituts für Ausgeflippten
Landmaschinenbau der Universität Hohenlohe.
Die Flächenmethode ist ein elegantes Verfahren zur Ermittlung des
Reaktionsergebnisses in Realen Reaktoren, von denen man das Verweilzeitspektrum
(aus Experimenten) kennt.
Ich muß Ihnen ehrlich gestehen, eine formale
Herleitung der Flächenmethode kann ich Ihnen nicht bieten. Gott sei dank
merkt man, wenn man sich mit der Materie befasst, daß die Formel der
Methode eigentlich sehr plausibel ist. Sehen wir es uns eben einmal an und
haben wir ein Augenmerk für den Gültigkeitsbereich.
Die
Flächenmethode benützt die Formel:
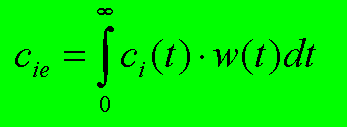
Formel für die
Flächenmethode
Wie wir ekennen, benötigen
wir die chemische Reaktionskinetik: ci(t) und die
Verweilzeitinformation des Reaktors: w(t). Das Integral in der Formel legt die
Erwartung nahe, daß man mit einer Flächenintegration (vor allem
graphisch) die Lösung für die Konzentrationsabnahme im praktischen
Reaktionsapparat erhalten könnte, - und so ist es auch !! Die
Flächenmethode ist also die graphische Auswertung der obigen Formel, -
selbstverständlich wäre auch ebenso eine rein numerische Auswertung,
z.B. auf einem Computer, möglich. Die Methode erlaubt uns - wie gesagt -
das Reaktionsergebnis (erreichbarer Umsatz) in einem Realen Reaktor bei
bekannter Kinetik und ermittelter Verweilzeitkurve des Reaktors zu berechnen.
Der Vorteil der Methode ist, daß sie mit jedem Realen Reaktor
funktioniert, wenn nur dessen Verweilzeitspektrum bekannt ist.
Betrachten
wir die graphische Lösungsmethode :
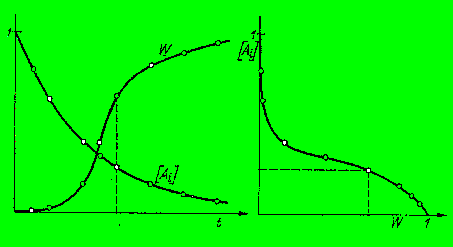
Flächenmethode,
graphische Lösung
Für dei graphische Auswertung müssen wir
korrespondierende Werte für c(t) und w(t) für gleiche Zeiten
aufnehmen ( am besten gleich genormte Werte W(t): 0-1 und
Ai/Ai0: 0-1 ). Diese Werte trägt man dann in einer
neuen Graphik gegeneinander auf. Das Reaktionsergebnis ist dann die Fäche
unter dieser Kurve. (Anm.: nicht die Rechteckfläche (!!!) in der
Abbildung, diese soll nur beispielsmässig 2 korrespondierende Werte
zeigen.)
Das scheint doch recht praktisch, oder ?
Ja, - aber, wenn 'alles so gut' ist, gibt es da sicher
einen Wermutstropfen !!!
Wenn wir uns die Formel und damit die Methode plausibel
machen wollen, finden wir den Wermutstropfen. Wir können hin und her
überlegen wie wir wollen und kommen endlich zum Schluß, daß
die Formel nur plausibel wird, wenn wir annehmen, die Reaktionsmasse sei ein
segregiertes Fluid und nicht etwa molekulardispers. Lassen Sie mich das so
formulieren: die Bildung eines Integrals über die Produkte von
'individuellen' Konzentrationen und 'individuellen' Verweilzeiten geht ja nur,
wenn wir diese 'Individuen' unterscheiden (diskriminieren) können.
Für ein molekulardisperses Fluid geht das nicht. Auf der anderen Seite
können wir uns modellhaft vorstellen, wir hätten in einem
Segregierten Fluid einen 'Schwarm' mikroskopisch kleiner AIKs vorliegen, die
innerhalb des 'großen Reationsgefässes' keinen Stoffasutausch
untereinander haben. Das bedeutet dann ja, daß unsere Reaktion in jedem
Mikro-AIK einen individuellen Konzentrationsverlauf annimmt, der durch die
Reaktionskinetik gegeben ist. Jeder Mikro-AIK hat zugleich eine individuelle
Gesamt-Reaktionsdauer, die seiner Aufenthaltszeit im 'großen Reaktor'
entspricht. Die Summe (das Integral) über alle Mikro-AIKs ergibt das
Reaktionsergebnis. Das erscheint doch plausibel, oder ?
Da wir
uns die Flächenmethode nur für Segregierte Fluide plausibel machen
können, müssen wir auch annehmen, daß die Methode
strenggenommen nur unter dieser Voraussetzung gilt.
Deshalb müssen wir uns im folgenden Gedanken
darüber machen, wie groß der Fehler sein wird, wenn wir die Methode
bei Vorliegen eines molekulardispersen Reaktionsfluids anwenden. Gibt es
riesige Unterschiede ?
Zur Genauigkeit, - und: 'der zweite
Ordnung-Effekt'
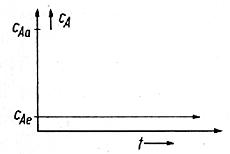
Stellen Sie sich vor, wir würden eine einfache
Reaktion A -> B in einem KIK durchführen, - denken Sie beispielsweise
an die Zersetzung eines roten Farbstoffes. Zuerst soll ein molekulardisperses
Reaktionsfluid vorliegen. Die Reaktionsgeschwindigkeit ist dann proportional
zur sehr niedrigen 'Restkonzentration' an Farbstoff im Kessel sein. Die
Raumzeitausbeute ist niedrig, größere Umsatzwerte können nur
mit großen Raumzeiten erreicht werden. Das könnte ein wenig wie im
folgenden dargestellt aussehen:
und, - wie gesagt: 'rein und runter'
Lassen Sie uns auf der anderen Seite ein segregiertes
Fluid nehmen. Mit einem 'virtuellen Zoom' betrachtet könnte das ein wenig
wie im folgenden Bild aussehen (wenn wir die Mikro-AIKs fiktiv
vergrößern):
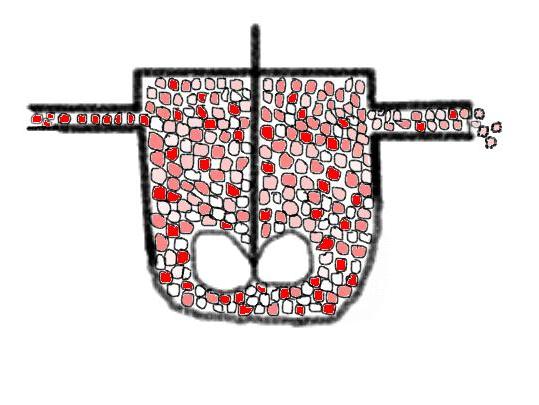
wenn Sie mit den Augen kneifen, daß das Bild etwas
verschwimmt, sehen Sie, daß die Farbintensität etwas höher ist
als im obigen Bild. Das bedeutet, wir haben im vorliegenden Fall eine etwas
höhere Eduktkonzentration als treibende Kraft für die
Reaktionsgeschwindigkeit.
Das bedeutet also, daß wir in segregierten
Fluiden immer eine etwas höhere mittlere Triebkraft 'Eduktkonzentration'
vorliegen haben als in molekulardispersen Fluiden. Das Reaktionsergebnis in
segregierten Fluiden ist genauer gesagt bei positiven Reaktionsordnungen immer
eine wenig besser und bei negativen Ordnungen ein wenig schlechter als
dasjenige in molekulardispersen Systemen.
In der Praxis zeigt sich aber, daß der Fehler der
hierbei gemacht wird, viel geringer ist als Fehler in der Ermittlung der
Verweilzeit, - es werden Werte unter 10% erwähnt. Für Reaktionen von
1.Ordnung kann man in der Praxis die Unterschiede fast nicht bemerken, weil der
mittlere Konzentrationseffekt nicht so groß ist. Nur für Reaktionen
höherer ( vor allem 2.Ordnung !!) oder niederer Ordnung können
größere Effekte auftreten und in der Praxis beobachtet werden. Es
gibt dazu sogar Versuche mit Durchführung derselben Reaktion im
molekulardispersen und im segregierten System.
| So, lieber Leser, jetzt bin ich endgültig an einer Stelle
angekommen, wo ich einfach mit meinem 'möglichst formelfrei-Prinzip' am
Ende bin. Ich kapituliere!!!! Immerhin habe ich bis hierher (fast)
durchgehalten, und Sie, die Sie bis hierher vorgedrungen sind, könnten ja
trotzdem mal versuchen, weiterzumachen. Ich habe auch versucht, wenigstens
einige Bildchen zur Erklärung hinzuzufügen. |
Die Wärmebilanz
Warum ist die Wärmebilanz in Reaktoren so wichtig
für die Chemische Reaktionstechnik ?
Wenn der Reaktionsmasse
Wärme zugeführt wird oder aus ihr abgezogen wird, ändert sich
die Temperatur. Da die Reaktionsgeschwindigkeit sehr stark von der Temperatur
abhängt (Arrhenius-Gleichung !!!), erhalten wir als Konsequenz eine
beträchtliche Änderung der Reaktionsgeschwindigkeit. Da
beispielsweise bei exothermen Reaktionen die produzierte Reaktionswärme
proportional zur Reaktionsgeschwindigkeit ist, erhalten wir für exotherme
Reaktionen im absatweisen Betrieb (batch) eine zunehmende
Reaktionswärme-Entwicklung. Dies führt wiederum zu einer
Temperaturerhöhung in der Reaktionsmasse, was wiederum zu .......Sie
merken: Stoff- und Wärmebilanz einer chemischen Reaktion, die in einem
Reaktor abläuft, sind miteinander verkoppelt, und eine simultane
Lösung beider Bilanzen zusammen könnte möglicherweise
kompliziert werden.
Aber lassen Sie uns zunächst einmal eine
'allgemeine Form' einer Wärmebilanz aufstellen ! In Analogie zur
Stoffbilanz können wir schreiben:
'Beobachtbare' Wärmeänderung
(Potentialgröße Temperatur)
durch 'Zufluß' zur oder 'Abfluß' aus der Reaktionsmasse
= Instationärer Term |
= |
Wärme,
die dem Reaktor im
Zustrom zugeführt wird
( 'Zulauf-Teil' des
Konvektiven
Terms) |
- |
Wärme,
die dem Reaktor im Ablauf
entnommen wird
( 'Ablauf-Teil' des Konvektiven Terms) |
+/- |
Wärme,
die von der Chemischen Reaktion
produziert oder verbraucht wird
( Reaktions-
term) |
Wärme,
die mit
der Umgebung ausgetauscht wird, durch Wärmeübergang,
Wärmeleitung und Strahlunswärme, - normalerweise durch
Wärmetransport durch der Reaktorwände |
| Term I = Instationärer Term
(oder auch 'Beobachtungsterm' ) |
|
Term IIa = Zulauf-Teil
des
Konvektiven Terms ( IIa + IIb ) |
minus |
Term IIb = Ablauf-Teil des
Konvektiven
Terms( IIa + IIb ) |
plus/minus |
Term III = Reaktions-
Term |
Term IV = Austauschterm |
'allgemeine' Wärmebilanz ( in Textform)
und wenn wir das in Formeln umsetzen:
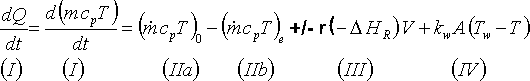
'allgemeine' Wärmebilanz in Termform
| Legende: Q = Wärme, T = Temperatur, t = Zeit, m
= Masse (z.B. kg) , m(Punkt) = Massenstrom (z.B. kg/sec), cp =
specifische Wärme, V = Reak-tions(-tor) Volumen, r =
Reaktionsgeschwindigkeit (konzentrationsabhängig), ΔHR =
Reactionsenthalpie, kw = Wärmedurchgangskoeffizient, A =
Austauschfläche (Reaktorwände), Tw = mittlere Zulauftemperatur des
Tauscherfluids (Wärmeträger, Kälteflüssigkeit). |
Lassen Sie uns nun in Analogie zur Stoffbilanz für
unsere verschiedenen Reaktortypen die verschiedenen Wärmebilanzen
aufstellen. Zunächst müssen wir aber die verschiedenen thermischen
Betriebsweisen in der Reaktionstechnik vorstellen !
Chemische Reaktoren können in folgenden thermischen
Betriebsweisen gefahren werden:
- der adiabatische Betrieb
- der isotherme Betrieb
- der polytrope Betrieb
Was bedeutet das ?
adiabatisch bedeutet, daß es keinen
Wärmetausch mit der Umgebung gibt. Aber im Gegensatz zur 'rein
physikalischen' Definition von adiabatisch, - ein Zustand, der in der
Reaktionstechnik nur im adiabatischen AIK realisierbar ist - bedeutet
adiabatisch in der Reaktionstechnik 'ohne Wärmeübertragung
über den Austauschterm', - wohingegen ein Wärmetransport
über den Konvektiven Term erlaubt sein soll. Dies erfolgt aus praktischen
Gesichtspunkten und ist in der Augen der 'sauberen Physik' etwas
willkürlich. Für Puristen zum Trost: der adiabatische AIK stellt -
wie bereits erwähnt - ein echtes adiabatisches System dar: But as
mentioned, realize that the adiabtic STR exhibits a really adiabatic system:
'ein Pot mit beispielsweise einer Styropor-Umantelung als Isolation' = ein
(beinahe) vollständig geschlossenes System !!!
Manchmal werden die beiden anderen thermischen
Betriebsweisen unter dem Begriff 'nichtadiabatische Betriebsweisen'
zusammengefasst !! Ihre gemeinsame Eigenschaft ist, daß sie
Wärmeaustausch mit der Umgebung beinhalten.Isotherm
bedeutet, daß die Wärmeflüsse derart bewerkstelligt werden,
daß die Reaktionsmasse auf einer konstanten Temperatur gehalten wird.
Dies kann durch eine externe Regelung erreicht werden oder durch einen
Automatismus in der Prozeßführung, wenn z.B. in einem
stationären Zustand die erzeugte Reaktionswärme genau passend durch
die Konvektion abgezogen wird. Die polytrope Betriebsweise ist
etwas vielseitiger als die isotherme. Polytrop bedeutet, daß die
Temperatur der Reaktionsmasse über Raum und Zeit betrachtet einer Art
Programm folgt. Der Bedarf an 'Regelungspower' eines solchen Systems ist
natürlich ziemlich groß und es ist erstaunlich, daß es gerade
hier doch auch einige Möglichkeiten von Automatismen ohne Erfordernis
einer externe Regelung gibt, - man trifft das z.B. bei einer autothermen
Führung in Rohrreaktoren an, wo die zulaufende Reaktionsmischung in
einem konzentrischen Gegenstrom-Doppelrohrwärmetauscher von der
ablaufenden Reaktionsmasse erwärmt wird.

Hier eine Übersichtstabelle für die 3
Betriebsweisen:
| Betrieb |
Charakteristik |
Probleme |
Vorteile |
| isotherm |
die Reaktionsmasse wird zwangsläufig auf eine
konstante Temperatur gehalten durch Wärmetausch oder Konvektion
|
schwierig zu regeln (Anm.: denken Sie z.B. an die
'Parametrische Empfindlichkeit in Rohrreaktoren', siehe Lit. /3/) |
einfache Reaktor-Auslegung |
| adiabatisch |
kein Wärmetausch mit der Umgebung, Wärme
kann in kontinuierlichen Reaktoren nur durch die Konvektion abgezogen
werden |
die Wärmeentwicklung kann leicht zu hoch
geraten
Reaktor-Auslegung etwas schwieriger |
keine aufwendige Regelung, höchsten
'Notabschaltung' |
| polytrop |
'Fahren' einer Art 'Temperatur-Programms' mithilfe
von Regelungen oder autothermer Prozeßführung |
schwierige Reaktor-Auslegung und regeltschnisch
eventuell aufwendig |
'saubere zonale Führung' der
Reaktion |
As an additional information on the various forms of
heat balances for our reactors take a blackboard sketch .
Nähere Beschreibung der thermischen Betriebsweisen in den
einzelnen Reaktortypen
-
adiabatische Reaktoren
- die adiabatische Temperaturerhöhung
Wenn Sie die adiabatische Betriebsweise 'auf die allgemeine
Wärmebilanz für exotherme Reaktionen anwenden' , müssen Sie
den Wärmetausch-Term entfallen lassen. Wenn Sie in der Formel desweiteren
alle Konzentrationswerte durch den Umsatz U substituieren und damit den
Reaktionsfortschritt - sozusagen genormt - mit U ausdrücken, erhält
man zunächst erstaunlicherweise (aber auch erfreulicherweise) für
alle 3 idealen Grundreaktortypen das selbe Ergebnis:
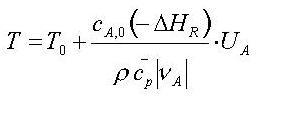
die adiabatische
Temperaturerhöhung
| Legende: UA = Umsatz der
Bezugskomponente, ΔHR = Reaktions enthalpie, T =
Endtemperatur, T0 = Starttemperatur, cp = specifische
Wärme, ρ = Dichte, cA,0 = Anfangskonzentration |
In Kurzform kann man schreiben: T =
T0 + Tad*U
in dieser Form sollten Sie sich den
Zusammenhang der adiabatischen Temperaturerhöhung merken, zusammen mit der
Tatsache, daß Tad proportional zur Reaktionsenthalpie und der
Anfangskonzentration der Bezugskomponente (z.B. Edukt) ist.
Die Formel sagt uns, daß die adiabatische
Temperaturerhöhung der Reaktionsmischung linear proportional zum Umsatz U
ist. Ist das so erstaunlich, daß dies für alle Reaktortypen gilt ?
Denken Sie einmal daran, wo die Reaktionswärme hingeht !! Sie geht in die
Reaktionsmasse, - und wenn es keinen weiteren Wärmetausch mit der Umgebung
gibt, geht sie ja auch wirklich 'einzig und alleine' in die Reaktionsmasse. Und
da ja die produzierte Wärmemenge pproportional zum Reaktionsfortschritt
(also Umsatz) ist, erhalten wir ja genau die Wärmemenge, die diesem
Reaktionsfortschritt entspricht - und nicht mehr !! Die 'Art', wie die
Wärme in die Reaktionsmasse übergeht, ist typisch für den
jeweiligen Reaktortyp:
Im Falle des AIK erwärmt sich die
Reaktionsmasse stetig mit dem Fortschritt der Reaktion und endet, wenn die
Reaktion abgestopt wird (beendet).
Im Fall des stationären IRs
wärmt sich die Reaktionsmasse stetig entlang der Rohrlänge auf, - im
gleichen Sinne, wie sich ja der Umsatz ändert. Und damit haben wir die
gleiche Situation wie bei der Stoffblanz: eine
Raum-/Zeit-Koordinatentransformation beim Übergang vom AIK zum IR und
umgekehrt !!
Im Falle des KIK haben wir einen simultanen, glechbleibenden
Ux 'überall im Pot', und die Reaktinsmasse wird unmittelbar auf
den Endwert 'adiabatische Endtemperatur' aufgewärmt:
T0 +
Tad* U.
Der Wert der adiabatischen Temperaturerhöhung
hat in der Praxis große Bedeutung: er stellt die maximale Temperatur dar,
die in einem Reaktor bei vollem Umsatz U = 1 erhalten wird, oder er gibt uns
ebenso den Maximalwert bei einem gegebenen Umsatz (<1) , das ist für
Regelungs- und Sicherheits-Aspekte wichtig.
Die Herleitung der Formel
für die adiabatische Temperaturerhöhung - das heißt, der
formale Beweis der obigen Angaben - ist ein Fall für die Übungen in
Technischer Chemie. Interessierte finden sie
hier (pdf-file, leider Englisch, aber
Formel bleibt Formel!))
Wichtig noch:
interpretieren Sie die Tatsache, daß die Temperatur linear mit dem Umsatz
steigt nicht falsch indem Sie daraus folgern, daß die Temperatur damit
auch linear mit (Rohr-)Länge und Zeit steige ! Denken Sie daran, daß
der Umsatz sich nicht linear mit der Zeit ändert (selbst im isothermen
Fall !!)
- Nun zu den drei
Grundreaktortypen -
- der adiabatische AIK
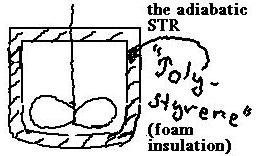
in der allgemeinen Wärmebilanz sind zu
setzen:
Wärmeaustausch-Term = 0
Konvektions-Term = 0
Das
ergibt ?? (Sie sollten das ausformulieren können!!)
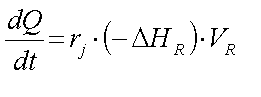
die Wärmebilanz im
adiabatischen AIK
das führt - wie oben gezeigt
- zur adiabatischen Temperaturerhöhung:
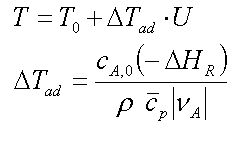
die
adiabatische Temperaturerhöhung
zur
Wiederholung: die Raumzeit ist repräsentativ für die Stoffbilanz.
Nur können wir hier im adiabatischen Fall nicht mehr, wie für den
isothermen Fall zuvor, nur r(U) einsetzen. Wir müssen jetzt auch noch
berücksichtigen, daß sich r mit u und T ändert. Wir sehen hier
schon die Verkoppelung von Stoff- und Wärmebilanz und können erahnen,
daß uns die gemeinsame Lösung nicht ganz so einfach 'zufliegt'.
Darauf werden wir dann im folgenden Kapitel eigehen dürfen
müssen.
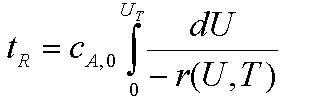
die
Raumzeit für den AIK
Kontrollfrage:
Wie können wir formal aufzeigen, daß im vorliegenden
Fall 'die Reaktionswärme in die Reaktionsmasse geht' ?
ganz einfach:
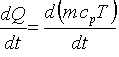
ok
?
- der stationäre adiabatische
KIK
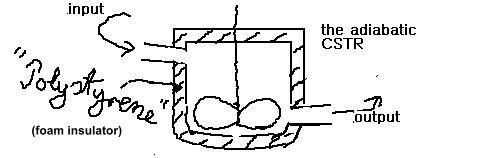
in der allgemeinen
Wärmebilanz sind zu setzen:
Wärmeaustausch-Term =
0
Instationärer Term = 0
Das ergibt ?? (Sie sollten das
ausformulieren können!!)
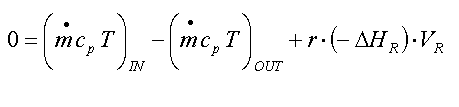
die Wärmebilanz des
stationären adiabatischen KIKs
man erhält
bei der Herleitung - wie oben erwähnt - die gleiche Formel für die
adiabatische Temperaturerhöhung:
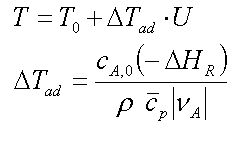
die
adiabatische Temperaturerhöhung
ebenso gilt
für die Raumzeit - r(U,T) nicht vergessen -
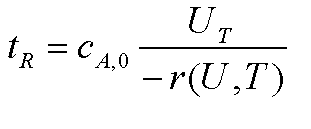
die
Raumzeit im KIK
auf die gemeinsame Lösung von
Stoff- und Wärmebilanz werden wir - wie gesagt - im nächsten Kapitel
eigehen.
- der stationäre adiabatische
Rohrreaktor

in der allgemeinen Wärmebilanz sind zu
setzen:
Wärmeaustausch-Term = 0
Instationärer Term =
0
Das ergibt ?? (Sie sollten das ausformulieren
können!!)
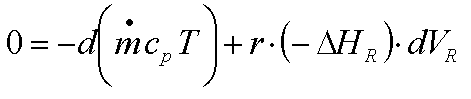
die Wärmebilanz für ein differentielles
Volumenelement des stationären adiabatischen IRs
man erhält bei der Herleitung - wie oben erwähnt - die
gleiche Formel für die adiabatische
Temperaturerhöhung:
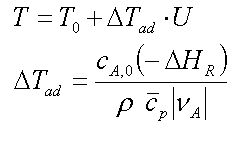
die
adiabatische Temperaturerhöhung
ebenso gilt
für die Raumzeit - r(U,T) nicht vergessen -
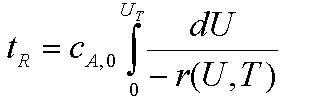
die
Raumzeit in einem IR
auf die
gemeinsame Lösung von Stoff- und Wärmebilanz werden wir - wie gesagt
- im nächsten Kapitel eigehen.
-
nicht-adiabatische Reaktoren
in
nicht-adiabatischen Reaktoren müssen wir zusätzlich den
Wärmeaustausch -Term berücksichtigen.
- der AIK mit Wärme-Austausch
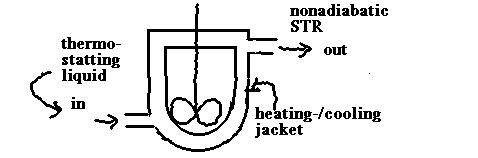
in der allgemeinen Wärmebilanz ist zu
setzen:
Konvektiver Term = 0
Das ergibt ?? (Sie sollten das
sebst ausformulieren können!!)
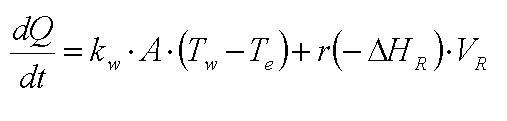
die
Wärmebilanz des nichtadiabatischen AIK
und zum
n-ten mal: die Raumzeit für die Stoffbilanz:
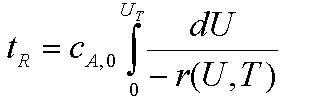
Raumzeit
für den AIK
Aber jetzt
kommt's: In Abhängigkeit von der Art und Weise, wie wir den
Wärmetausch-Prozeß handhaben, unterscheidet man zwischen dem
isothermen Betrieb und dem polytropen Betrieb. Das beeinflußt die Form
der 'allgemeinen' Wärmebilanz in unserem nichtadiabatischen AIK, bzw. es
'fließt' in die Formel ein.
- bei der isothermen Betriebsweise 'zwingen'
wir das System zu einer konstanten Temperatur. Als Folge davon finden wir kein
beobachtbares dQ/dt., - der Instationäre Term wird Null. Es folgt
also:
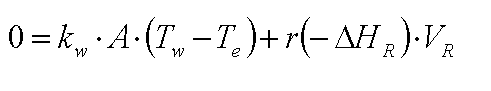
die Wärmebilanz für den isothermen
AIK
- bei der polytropen Betriebsweise lassen wir
ein beobachtbares dQ/dt zu, d.h. wir führen ein Temperatur-Programm aus,
das wir durch eine ständige Kontrolle des Wärmeaustauschvorgangs
verifizieren. In diesem Fall gilt der 'volle Ansatz' der 'allgemeinen'
Wärmebilanz ( siehe oben).
Bei beiden Betriebsweisen müssen wir
für den Wärmeaustauschprozeß einen Kontrollvorgang
etablieren.
(auf die gemeinsame
Lösung von Stoff- und Wärmebilanz werden wir - wie gesagt - im
nächsten Kapitel eigehen.)
- der stationäre KIK mit
Wärme-Austausch
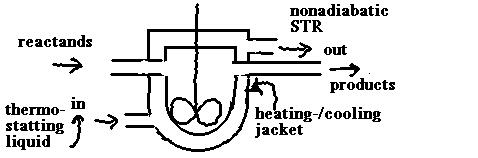
in der allgemeinen Wärmebilanz ist zu
setzen:
Instationärer Term = 0
Das
ergibt ?? (Sie sollten das sebst ausformulieren
können!!)
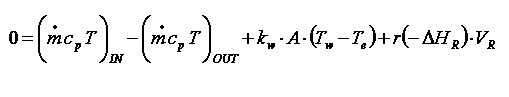
die Wärmebilanz im nichtadiabatischen
KIK
und die Raumzeit:
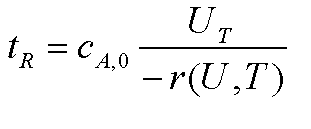
die
Raumzeit im KIK
- isotherm / polytrop
-
Im Falle des KIK beeinflußt die
Betriebsweise 'isotherm oder polytrop' die Wärmebilanz nicht. Für die
isotherme Betriebsweise ist das augenfällig, wir müssen da ja die
drei Terme der Bilanz so ausbalanziert halten, daß die Temperatur
konstant bleibt. Das erreicht man mit Hilfe der Lösung einer einfachen
algebraischen Gleichung (was ja die Konsequenz des Entfallens des
Instationären Terms und damit des Differentials - sprich der
Differentialgleichung - ist. Wie ist das aber beim polytropen Betrieb ? Hier
wird ja die Temperatur des Reaktorsystems verändert, wieso soll es da
keine Änderung in der Wärmebilanz geben ? Ich versuche das so zu
erklären: 'jeder momentane Betriebszustand im polytropen Ablauf ist als
'momentan stationär' aufzufassen. Damit ist der polytrope Betrieb im AIK
eine 'Aneinanderreihung' isothermer Betriebspunkte, die sozusagen als
'Zeitscheibchen' aufgereiht sind.
Wir sehen also letztlich: beide
Prozeduren können im KIK ohne größere Regeltechnische Probleme
verwirklicht werden. Nur, Sie wissen ja, der 'standalone' KIK ist im Normalfall
kein optimaler Produktionsreaktor.
- das IR mit Wärme-Austausch
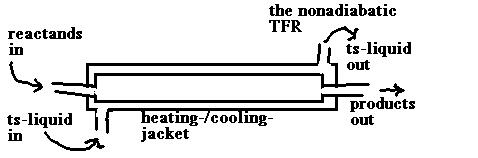
in der allgemeinen Wärmebilanz ist zu
setzen:
Instationärer Term = 0
Das ergibt ??
(Sie sollten das sebst ausformulieren können!!)
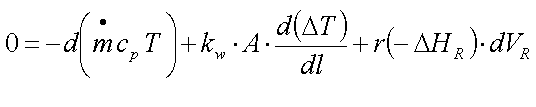
die Wärmebilanz im
nichtadiabatischen IR
und für die Raumzeit:
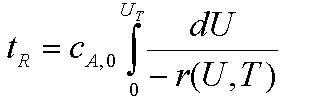
die Raumzeit im IR
Wie Sie aus der
Formulierung der Wärmebilanz für das IR mit Wärmeaustausch
erkennen, bleibt uns da - trotz des stationären Zustands - die
mathematische Form einer Differentialgleichung erhalten. Die
Differentialgleichung 'repräsentiert' das Vorhandensein eines Gradienten -
hier in der Temperatur - entlang dem Volumen, bzw. der Länge des Rohrs.
Deshalb wird die Lösung der Bilanzgleichung schwieriger. Im Falle der
polytropen Betriebsweise wird es noch komplizierter, weil der partielle
Wärmeaustausch-Term kw*A*d(deltaT)/dl stetig angepasst werden
muß. Außerdem spielen hier weitere
Wärmestrom-Führungs-'Spielarten', wie Gleichstrom- und
Gegenstrom-Betrieb eine wichtige Rolle.
Es verwundert einen deshalb nicht,
daß in nichtadiabatischen Rohrreaktoren scheinbar 'irrationale'
Verhaltensweisen, wie z.B. die 'berühmte' Parametrische Empfindlichkeit ,
beobachtet werden können. (interessiert ? siehe Lit. /3/ ).
Und, was uns ja jetzt schon klar ist: es ist zu
erwarten, daß die simultane Lösung von Stoff- und Wärmebilanz
des IRs mit seinen Konzentrations- und Temperatur-Gradienten entlang der
Rohrlänge noch komplizierter wird. Wir werden uns deshalb im folgenden
Kapitel nur mit einfachen und verständlichen Beispielen 'begnügen'
müssen.
Hiermit haben wir die
Grundsteine für das folgende Kapitel gelegt.
und so geht's weiter
:
Simultane Lösung von Stoff- und Wärmebilanz
- adiabatische Reaktoren
Reaktionen in:
- der adiabatische AIK
- der adiabatische KIK
- das adiabatische IR
- nicht-adiabatische
Reaktoren
ReaKtionen in:
- einem AIK mit Wärme-Austausch
- einem KIK mit Wärme-Austausch
- einem IR mit Wärme-Austausch
|
adiabatische Reaktoren
Die simultane graphische Lösung von Stoff- und Wärmebilanz in
adiabatischen Reaktoren
Bei der adiabatischen Reaktionsführung gilt - wie
bereits erwähnt - die lineare Abhängigkeit der adiabatischen
Temperaturerhöhung vom Umsatz für alle Reaktortypen. Wir können
deshalb für alle Reaktortypen einen linearen Graphen der Reaktortemperatur
in Abhängigkeit vom Umsatz anlegen, dabei liegt die Start-TemperaturIt
T0 auf dem Y-Achsen-Abschnitt (T- Achse!). Wenn wir in den selben
Graphen mit einer zusätzlichen Y-Achse für die 1/r - Funktion den
Plot 1/r(U,T) = f(U) einzeichnen, hier - wie bereits erwähnt -
für r(U,T), - dann können wir unsere Raumzeit im 1/r - Plot in
gleicher Weise wie im Falle der Stoffbilanz für isotherme Reaktionen
alleine ermitteln. Wir müssen für die 1/r(U,T) - Kurve nur bestimmte
U-Werte suchen, ihre zugehörigen T-Werte aus der Geraden entnehmen und mit
ihrer Hilfe den zugehörigen k-Wert berechnen ( Arrhenius!!). Aus dem
k-Wert berechnen wir dann schließlich den Wert für die
Reaktionsgeschwindigkeit r. Für eine Reaktion 1. Ordnung wäre das
z.B. r = k(T)*CA,0*(1-U).
sehen wir uns solch einen Graphen
für eine irreversible exotherme Reaktion erster Ordnung
an:
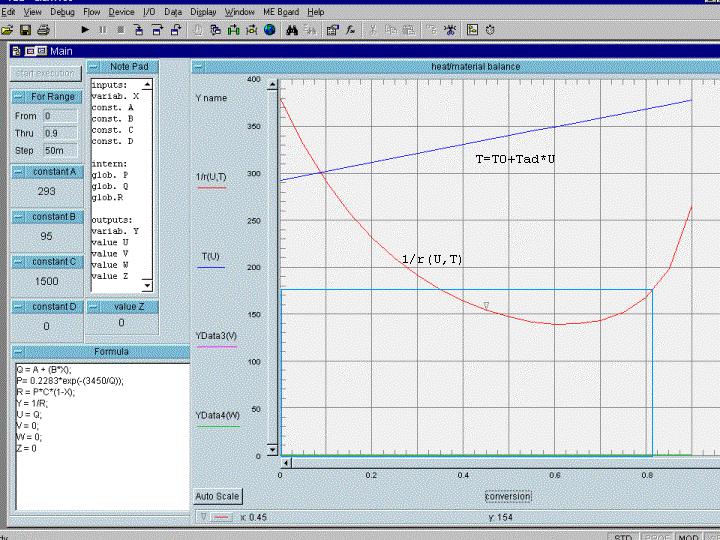
die Daten: k = 0.2283 exp(-3450/T) 1/sec,
CA,0 = 1500 mol/m3, delta Tad= 95 K,
T0= 293 K
Wirklich auffallend und interessant ist hier der im
ersten Umsatzbereich fallende Zweig der 1/r-Kurve. Da ja die Raumzeit für
nicht-rückvermischte Reaktoren das Integral für die Fläche unter
der Kurve ist, müssen wir realisieren, daß im vorliegenden Fall
diese Reaktoren in diesem Bereich nicht so gut sind wie der KIK
(Rechteckfläche !!). Bis etwa 75% Umsatz ist der KIK besser (siehe
'blaues' Rechteck). Die beste Lösung wäre hier wieder - wie bei der
Autokatalytischen Reaktion - eine Reaktorschaltung. Wir haben also ein weiteres
Beispiel, bei dem die reine umsatzorientierte Optimierung (mit Verwendung
nicht-rückvermischter Reaktoren) nicht von Vorteil ist.
 -----
15.03.06
-----
15.03.06
Fortsetzung folgt
!!
zurück zu Teil 1
zurück zu Teil 2
zurück zu Teil 3
Bitte teilen Sie mir mit, wenn ein Interesse am vorliegenden Stoff
besteht ! Ganz toll wäre auch, wenn ich auf Fehler aufmerksam gemacht
würde.
zur
Homepage des Autors