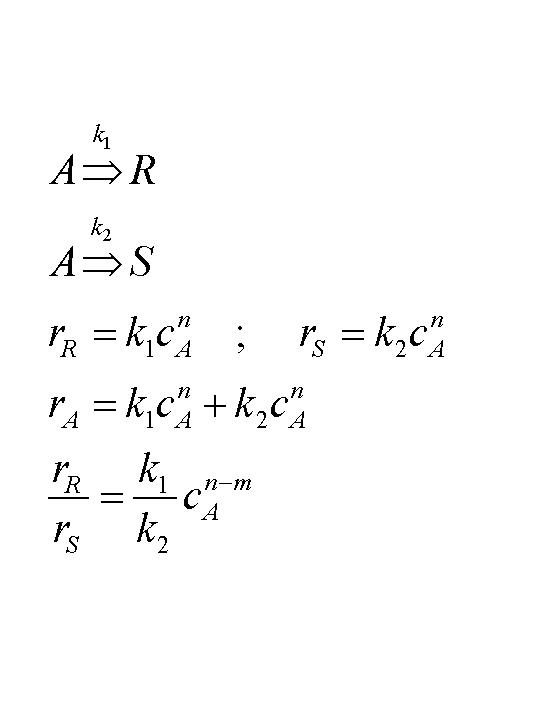Fortbildung für technisch interessierte Laien: 'Was ist chemische
Reaktionstechnik?' - Teil 2
zurück zu Teil 1
zur
Homepage des Autors
'Zwischen Durchflußrührkessel und Rohr'
Na ja, wenn wir schon bei den Verwandtschaften sind, - gibt es denn gar
nichts, womit man die beiden kontinuierlichen Reaktortypen KIK und IR
miteinander 'verschwägern' könnte ?
Doch es gibt ! Über das Zauberwort 'Reaktorschaltungen' . Wir
betrachten hier einmal im Vorgriff die Serienschaltung von
Durchfluß-Rührkesseln. Diese Anordnungen werden Rührkessel-Kaskaden oder einfach nur
Kaskaden genannt.
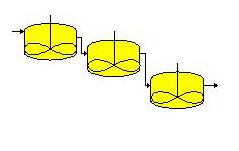
Stellen wir uns doch einmal rein optisch die Hintereinanderschaltung von
immer mehr Rührkesseln gleichen Volumens vor, - aber derart, daß das
Gesamtvolumen = n mal Einzelvolumen konstant bleibt. Die Kessel werden dann ja
mit zunehmender Kesselzahl immer kleiner und die 'Perlenkette' immer
länger und schlanker'. An was erinnert uns das? Sind das nicht so kleine
Scheibchen-Zellen wie im IR? Können wir vielleicht sagen, eine Kaskade mit
n Durchflußrührkesseln nähert sich mit zunehmender Kesselzahl n
dem Strömungsrohr. Ja, wir können !! Und es soll schon an dieser
Stelle nicht verheimlicht werden, daß
oft schon eine Kaskade mit wenigen Kesseln ( so um 3 Stück etwa!!)
für ein viel besseres reaktionstechnisches Ergebnis ausreicht.
So, jetzt kommt die Stunde der Wahrheit und ich muß zugeben, ich
sitze jetzt recht kräftig in der Tinte. Wie soll ich Ihnen nur in
Wort und eventuell 'noch ein wenig in Bild' die halbe Physikalische Chemie
vermitteln? Meine Berufskollegen werden sich jetzt diebisch freuen, warum hat
er auch eingangs 'das Maul so voll genommen' !! Es sind da folgende Themen zu
erörtern:
- Stöchiometrie Chemischer Reaktionen
- Thermodynamik Chemischer Reaktionen
- Kinetik Chemischer Reaktionen
- Mechanismus Chemischer Reaktionen
Eine Bitte habe ich jetzt wenigstens an meine Kollegen: haben Sie
Nachsicht mit mir !! Die, die mich kennen, werden sowieso denken: "na ja, der
war noch nie ein 'gscheiter' Chemiker", womit sie sicher recht haben. Aber oft
kann's der 'Doofie' dem anderen besser erklären !! (siehe "...für
Dummies"-Serie in der Computer-Literatur). Und als Trost für Sie, lieber
Leser, der andere kann ja dabei durchaus auch 'gscheiter' sein.
Also, los geht's:
Reaktionsmechanismus
Fangen wir zunächst mal sofort an mit dem Blick in die Mikrowelt
der Atome und Moleküle und versuchen, den Begriff Reaktionsmechanismus zu
ergründen. Da gehen wir ruhig etwas 'modellmässig' vor. Sie alle
wissen heute, daß Materie aus Atomen und Molekülen besteht. Stellen
wir uns nun modellmässig vor, wir haben in einem geschlossenen
Gefäß voll reinem Heliumgas (Edelgas -> Ballongas) einen
riesengrossen Schwarm mikrokleiner Kügelchen - und das seien die
Heliumatome. Die 'schwirren' da so im Behälter herum und das Tempo, mit
dem sie herumschwirren und wie oft sie 'zusammenstossen' wird durch die
Temperatur bestimmt (und 'macht den Druck aus' - für ganz Genaue!!), je
'heisser daß es zugeht', desto schneller schwirren die Atome herum und
desto öfter stoßen sie zusammen.
Mit dem
'Spezial-Vergrößerungsglas' könnte ein Gasgemisch dann etwa so
aussehen:

Aufgenommen im Crazy-Machines-Laboratory der
Chaos-University of Hohenlohe.
Ich denke jeder hat soviel Phantasie,
daß er das nicht so ganz ernst nimmt. Die 'Federteller' am Boden sind
sozusagen Wärmeenergiequellen, wohingegen an den starren Wänden ja
nur Impulsumkehr stattfindet.
Dann nehmen wir ein Becherglas voll
Wasser. Hier 'schwirren' jetzt Wassermoleküle herum. Wasser ist
H2O, d.h. ein Molekül, das aus 2 Atomen Wasserstoff und einem
Atom Sauerstoff 'zusammengebastelt' ist, - die Atome ebenfalls wieder als
Kügelchen modelliert, das Molekül aber als eine Art (geknickter oder
gestreckter) 'Hantel' aus den Kügelchen zusammengeklebt ( Kügelchen
eben = Wasserstoffatome und Sauerstoffatome ). Bei einer Reaktion werden nun
Bruchteile von Molekülen (also von Aggregaten von Kügelchen) mit
anderen Bruchteilen oder auch mit Atomen (also Einzelkügelchen)
'zusammentreffen' und 'im Reaktionsmoment mit 'Sekundenkleber' zu einem neuen
Gebilde (Molekül) verknüpft werden. Es können auch
Kugelaggregate (Moleküle) einfach in Bruchteile, - wie kleinere Aggregate
- oder nur noch Kügelchen zerfallen. Wie das alles abläuft, das sagt
uns der 'Reaktionsmechanismus'. Merke: die im folgenden beschriebene
stöchiometrische Reaktionsgleichung sagt zunächst gar nichts
über den Mechanismus, also den Ablauf der Reaktion aus.
|
Der Mechanismus einer Reaktion
sagt aus, in welcher Weise die Stoffe im atomaren und molekularen Bereich
miteinander raeagieren. |
|
Man kann nun verschiedene Typen von Reaktionen und Mechanismen
kategorisieren. Wir wollen hier nicht so ins Detail aller chemischen Reaktionen
gehen, daß wir jetzt alle Mechanismen und mechanistischen Teilschritte
von Reaktionen in der anorganischen und organischen Chemie aufführen und
diskutieren. Für die Reaktionstechnik wichtig, weil ausschlaggebend
für das 'Reaktionsergebnis im Reaktor', sind vor allem (und das sozusagen
mehr global gesehen): Hin- und Rückreaktionen und
ihr Gleichgewicht (hierzu auch im folgenden 'Thermodynamik'), Parallel- und
Folgereaktionen. Sie können sich vielleicht denken, daß wenn
wir in einem Reaktor eine 'Suppe mit vielen Ingredienzien kochen', daß da
auch vieles passieren kann. Es kann ein Stoff in einem Reaktionsschritt
gebildet werden, aber gleich darauf weiterreagieren zu einem nächsten
Stoff, dann hätten wir z.B. eine Folgereaktion vorliegen. Es könnte aber auch ein
Stoff A zerfallen und auf einem Reaktionsweg Stoff B bilden, gleichzeitig aber
auch auf einem anderen Weg Stoff C, - wir hätten dann eine
Parallelreaktion.
|
Elementare Reaktionstypen
können miteinander 'verschaltet' werden in sogenannten
'Reaktions-Netzwerken', von hauptsächlich Parallel- und
Folgereaktionen. |
|
Und hier sehen wir wieder die Bedeutung des Wesens der Chemischen
Reaktion für die Reaktionstechnik. Nehmen wir doch mal an, eine
Parallelreaktion liege vor und wir wollen nur Produkt B. Wann kann das
Parallel-Netzwerk mehr in Richtung B 'gepusht' werden, - kann da die Wahl des
Reaktors was ausmachen? Oder: wir haben eine Folgereaktion und wollen genau das
Zwischenprodukt 'abfangen', - was machen ?
Stöchiometrie und
Thermodynamik
Die meisten von Ihnen haben in der Schule gelernt:
HCl + NaOH < -
> NaCl + H2O. Das war Stöchiometrie, flapsig gesagt 'die
Mengenlehre der Chemie', oder der 'Buchhalter für die Massenbilanz der
Reaktion', denn Masse darf ja nicht ohne weiteres verlorengehen. Nach rechts
gelesen bedeutet das: wenn ich das Molekuargewicht in Gramm an Salzsäure
mit dem Molekualgewicht in Gramm an Natronlauge reagieren lasse, erhalte ich
das Molekulargewicht in Gramm an Natriumchlorid = Kochsalz (und Wasser). Jetzt
haben wir da aber einen Doppelpfeil in der stöchiometrischen
Umsatzgleichung. Ich kann auch nach links lesen, wenn ich das Molekulargewicht
an Kochsalz 'irgendwie ( in Wasser???) malträtiere (vielleicht gewaltig
'darauf herumbrate') erhalte ich das Molekulargewicht an Salzsäure und
dasjenige von Natronlauge (so Gott will, das wird sicher nicht so leicht
gehen!!). Daß das 'nicht so leicht' geht, dafür ist die
Thermodynamik der Reaktion verantwortlich.
Die Thermodynamik ist der 'Energiekommissar' der Chemischen Reaktion. Sie
bestimmt, ob eine Reaktion überhaupt in der oder jener Richtung
abläuft und in welchem Ausmaß - - man spricht hier vom
Gleichgewicht zwischen Hin- und Rückreaktion,
oder von der Gleichgewichtslage). Außerdem
z.B. auch noch: - wieviel Wärme ( allgemeiner: Energie, so z.B. auch
Lichtenergie) frei wird oder gebraucht/gebunden wird. Es sind hierbei vor allem
die 'Schlagwörter': Gleichgewicht der Reaktion, Reaktionswärme
(Reaktionsenthalpie) und Entropie der Reaktion (Reaktionsentropie) zu
nennen. ( Ganz laienhaft ausgedrückt ist die Entropie ein Maß
für die Wahrscheinlichkeit, daß ein Prozeß (z.B. eine
chemische Reaktion) in eine erwartete Richtung verläuft. Es gibt auch noch
andere 'Bilder' für die Veranschaulichung von Entropie, - so wie
beispielsweise das 'markige Statement' - die Entropie des Weltraums strebt auf
ein Maximum zu, - hier wird Entropie als Maß für die
Ordnung/Unordnung im System herangezogen. Sogesehen gilt das ja eigentlich auch
für menschliche Populationen und ihr wirtschaftliches und poltisches
Agieren !!)
|
Eine
Stöchiometrische Reaktionsgleichung sagt nur aus, wieviel Produkt aus
wieviel Ausgangsstoff auf dem 'formulierten globalen' Weg enstehen kann. Eine
Aussage darüber, wie die einzelnen mechanistischen Schritte der chemischen
Reaktion aussehen, gibt sie nicht. |
|
Reaktionskinetik
Schon eingangs habe ich erwähnt, daß für die Spezifische
Produktleistung die Schnelligkeit der Reaktion eine wesentliche Rolle spielt, -
also die Zeit, die eine Reaktion braucht. Das Gebiet, das sich mit dem
zeitlichen Ablauf der Reaktionen befasst, ist die Reaktionskinetik. Unter
Reaktionsgeschwindigkeit versteht man die zeitliche Änderung einer
Komponente, bei Produkten spricht man von 'Bildungsgeschwindigkeit', bei
Edukten von 'Verbrauchsgeschwindigkeit'. Bei experimentellen Untersuchungen des
zeitlichen Verlaufs der Konzentrationen von Reaktionskomponenten während
einer Reaktion konnte/kann man bestimmte Gesetzmässigkeiten feststellen.
Die Geschwindigkeit der Bildung oder des Verbrauchs ist oft von der
Konzentration dieses Stoffes und/oder der Konzentration anderer Komponenten
abhängig, - und es stellt sich heraus, daß diese Abhängigkeit
mit der 0ten bis meist nicht mehr als 3ten Potenz der Konzentration 'wirkt', -
gleichzeitig bestimmt aber auch noch ein Faktor, den man dann
Geschwindigkeitskonstante nennt, - das
Ausmaß mit dem die Konzentration 'wirkt'. Die Geschwindigkeitskonstante
ist also typisch für eine Reaktion und bestimmt grundsätzlich, wie
schnell diese verlaufen kann. Die Potenz mit der die Konzentration 'wirkt'
nennt man Ordnung. Man spricht also z.B. von
Reaktionen 1. oder 2. Ordnung. Nun wissen die Chemiker, daß bei
einfachen, oft 'eindeutig' genannten Reaktionen, - bei Reaktionen z.B. 1.
Ordnung ein sogenannter 'monomolekularer' Reaktionsmechanismus vorliegt,
bei dem also nur 1 Molekül sozusagen die Hauptrolle spielt. Das ist
beispielsweise oft der Fall, wenn ein Molekül A einfach zerfällt und
B bildet. Ebenso findet man viele 'bimolekularen' Reaktionen, bei denen
nach genau untersuchtem Mechanismus die zwei Komponten A und B miteinender
reagieren (z.B wenn die Moleküle zusammenstossen) und man 'misst' eine
Rektionskinetik, die von 1.Ordnung bezüglich A und von 1. Ordnung
bezüglich B ist. Man sagt dann, die Reaktionsordung hinsichtlich der
beiden Komponenten ist jeweils 1, die 'Brottoreaktionsordnung' aber ist 2.
Also: Molekularität und Ordnung sind bei einfachen, oder
besser eindeutigen Reaktionen gleich. Nun ist das leider nur der ideale
Ausnahmefall. Wie oben bereits erwähnt, können chemische Reaktionen
komplexe Netzwerke 'mechanistischer' Teilreaktionen sein und es ist eigentlich
plausibel, daß die daraus sich ergebenden Rektionskinetischen
Zusammenhänge formelmässig komplexer werden, ja es können sogar
Reaktionsordnungen mit negativen und gebrochenen Exponenten auftreten. Das
lässt sich formal zeigen, wenn man reaktionskinetische Formeln für
Abfolgen verschiedenster mechanistischer Teilschritte herleitet, - selbst wenn
diese alle 'frei erdacht' wären. Wie ist das alles zu bewerten und ein
wenig Ordnung in die Sache zu bringen? Fest steht: chemische Reaktionen laufen
nach bestimmten Mechanismen ab. Als Folge davon 'sehen' wir (durch Messungen)
eine Formel für die Kinetik der ablaufenden Reaktion. Bei einfachen
Reaktionen sind diese kinetischen Daten in Übereinstimmung mit einem - in
diesem Fall meist auch erforschten - Mechanismus. Bei komplexen Reaktionen
können wir unter Umständen nur die Reaktionskinetik messen, wissen
aber im Detail nichts über ablaufende Mechanismen, - dies genauer zu
erforschen ist die Aufgabe 'von Generationen' von Chemikern.
|
Kinetische Daten
beschreiben zunächst einmal nur den beobachtbaren zeitlichen Verlauf der
Reaktion. Sie sind allenfalls ein Indiz für irgendwelche
mechanistischen Annahmen. Mechanismen müssen vom Chemiker erforscht werden
und sollten eigentlich bei kompletter Erforschung eine Herleitung der
beobachtbaren Kinetik ermöglichen, - dies ist aber wegen der
Komplexizität oft nicht möglich. Kinetiken, die durch mathematische
Anpassung an Formeln, die sich rein formalmathematisch aus Annahmen über
Mechanismen herleiten lassen, erhalten werden, nennt man fachsprachlich
'Formalkinetiken'. Man könnte aber auch mit Fug und Recht sagen,
alle Kinetiken, die nicht mechanistisch 'hinterlegt' sind, haben formalen
Charakter. Es gelingt sogar auch wirklich recht oft, komplexe Kinetiken durch
Potenz(reihen)ansätze zu beschreiben. Nun, - ein Trost: dem Reaktor ist
der Mechanismus in der Regel 'wurscht' , - er braucht zum 'Arbeiten'
hauptsächlich die Kinetik und höchstens noch etwas nähere
Kenntnis über die Struktur des globalen Reaktionsnetzwerks. Die
Geschwindigkeit einer Reaktion ist proportional zur Geschwindigkeitskonstanten
und zu Komponentenkonzentrationen (mit verschiedensten Exponenten = (Formal-)
Ordnungen) |
|
Jetzt sind wir mit dem 'Wesen' der Reaktion schon wieder etwas
weitergekommen! Die Schnelligkeit der Reaktion ist nicht allein durch den
Reaktionstypus gegeben - repräsentiert durch die
Reaktionsgeschwindigkeitskonstante -, sondern es spielen auch die aktuellen
Konzentrationen verschiedener beteiligter Komponenten eine Rolle. Die
Gesetzmässigkeit hierzu gibt uns die reaktionskinetische Gleichung. Diese
kann experimentell ermittelt werden. Es ist sogar sehr plausibel anzunehmen,
daß wir reaktionstechnisch mehr durch die 'Führung der
Konzentrationen' im Reaktor erreichen werden als durch die
Geschwindigkeitskonstante, die ja im Normalfall eine schlecht zu
verändernder Eigenschaft der Reaktion sein wird.
| An dieser Stelle eine Literaturempfehlung von
ganz besonderer Art: falls Ihnen mein Stil hinsichtlich der Ausführungen
zum 'Wesen der Reaktion' noch nicht 'flapsig' genug war, d.h. wenn Sie noch ein
wenig mehr 'Cartooniges' erwartet hätten, dann empfehle ich Ihnen das
amerikanische Cartoon-Buch 'The Cartoon Guide to Chemistry' von L. Gonick und
C. Criddle, Literatur / 9 /. Als einzigen
Hinweis möchte ich in diesem Zusammenhang aber noch abgeben: ich stimme
mit der Rezension des Buchs in den GdCH-Nachrichten überein, daß der
absolut unvorgebildete Lernende mit dem Buch etwas überfordert sein
dürfte, - es ist eher für Leute gedacht, die das Ganze nochmals aus
einer anderen, 'launigeren' Warte heraus verinnerlichen wollen, - es ist dann
auch wirklich gut. |
|
Ach du lieber Himmel, vor
lauter "laß mich auch mit" hätte ich beinahe die physikochemisch
gesehen wichtigste Einflußgröße auf das Reaktionsgeschehen
vergessen , die Temperatur !! Die Temperatur beieinflußt
zum einen über die berühmte Formel zur Temperaturabhängigkeit
Chemischer Gleichgewichte die Lage des Gleichgewichts und damit, wieweit die
Reaktion überhaupt in die gewünschte Richtung verläuft (kennen
Sie die Formel ? wenn nein, schnellstens Lehrbuch für Physikalische Chemie
aufschlagen). Desweiteren hängt der Wert der
Reaktionsgeschwindigkeitskonstanten über die Arrhenius-Gleichung
exponentiell von der Temperatur ab. Es verwundert einen deshalb nicht, wenn der
Temperaturführung und dem Wärmehaushalt in Reaktoren ein extra
Kapitel gewidmet werden muß. |
|
Lassen Sie uns aber
zunächst im Folgenden die ganzen reaktionstechnischen Probleme für
den isothermen Betrieb betrachten, - also bei konstanter
Temperatur. |
Haben Sie jetzt etwa schon
'Formel-Entzugserscheinungen' ? Dann könnten wir ja an dieser Stelle ein
paar formale Reaktionsgleichungen, - so mit A gibt B und C etc. und einige
wenige kinetische Ausdrücke formulieren, die uns vielleicht später
von Nutzen sein könnten !! Außerdem wäre es sinnvoll, an dieser
Stelle die Begriffe: Umsatz, Ausbeute und Selektivität zu erläutern.
Ich habe mir überlegt, ob ich den Schein des 'Formelfreien' dadurch wahren
soll, daß ich Links zu Bildchen mit dem jeweiligen Inhalt setze, dann ist
das Ganze 'verkappt'. Aber haben wir das nötig ?
Konzentration
engl. concentration |
ci = ni/V |
i = i te Komponente
n = Molzahl |
Konzentration der Komponente i = Zahl der mole an i pro
Volumeneinheit z.B. mol/l |
Umsatz
engl. conversion |
Ui =
(cio-ci)/cio
Ui =
(nio-ni)/nio |
o
= zu Beginn der Reaktion, i = i te Komponente zum aktuellen
Zeitpunkt |
'Abnahme' an Komponente i in Bezug auf die 'Menge' an i zu Beginn
der Reaktion |
Ausbeute
engl. yield |
Aik = (cio-ci)/cko |
o
= zu Beginn der Reaktion, i = i te Komponente (Produkt) zum
aktuellen Zeitpunkt
k=Referenz-Edukt |
auf Anfangs-Eduktmenge bezogene Produktmenge |
Selektivität
engl. selectivity |
Sik = Aik/Uik |
i = i te Komponente (Produkt) zum aktuellen
Zeitpunkt
k=Referenz-Edukt |
wie groß ist die Ausbeute an Produkt i bezogen auf den Umsatz
des Referenz-Edukts |
| Raumzeitausbeute = spezifische Produktleistung |
mP/(tR.VR) |
mP = Masse an Produkt, tR = Raumzeit
(Reaktionsdauer),
VR = Reaktorvolumen |
Menge Produkt pro Raum und Zeit |
Anm.: die Formeln sind teilweise nicht ganz korrekt, sie gelten
eigentlich nur für 1/1 - Reaktionen, - es fehlen die
stöchiometrischen Verhältniszahlen (siehe hierzu z.B. Literatur /1/,
/2/ u. /3/)
Einige allgemeine Grundlagen zur
Reaktionskinetik
Reaktionsgeschwindigkeit. Lassen wir unseren 'virtuellen Lehrer'
eine allgemeine Formel für die Differentialgleichung eines einfachen
reaktionskinetischen Ansatzes formulieren.
Reaktionsgeschwindigkeit (Anm.:
Link nicht zur 'verkappten' Formeldarstellung, sondern zur Effekthascherei !!)
- zurück mit Browser-back !!!
Die Reaktionsgeschwindigkeit,
gleichzusetzen mit der differentiellen zeitlichen Zu- oder Abnahme einer
Komponente, ist abhängig von einer Reaktionsgeschwindigkeitskonstanten,
sowie von Komponentenkonzentrationen und deren Ordnungs-Exponenten ( also
nochmals: r = -dc/dt = k*Cn). Lösungen von
derartigen Differentialgleichungen ergeben in der Regel immer 'irgendwelche'
Exponentialfunktionen. / Für Insider: ich möchte mich (zumindest an
dieser Stelle) um die genaueren Formeldetails 'drücken' (z.B.
Abhängigkeit der Dimension der Geschwindigkeitskonstante von der Ordnung,
Aufzeigen der Lösungswege für diese kinetischen
Differentialgleichungen u.s.w.)./
Einfache Reaktionen von 1. und 2. Ordnung
Der zeitliche Konzentrationsverlauf von Komponenten während
einer Reaktion wird als Lösung der kinetischen Differentialgleichungen
erhalten (Sie wissen ja: im einfachsten Fall: Separieren --->
Integrieren!!).
Beispiel: einfache Reaktion 1.
Ordnung:
A > B ; Differentialgleichung: -dCA/dt = +
dCB/dt =
k * CA ---- Lösung:
CA = CAo* e(-kt) = exponentielle Abklingkurve für die
Ausgangskomponente A. (der Verlauf von CB ist durch
(CAo - CA) gegeben = exponentielle
Aufstiegskurve).
Wäre die Reaktionsordnung 2, hätten wir die
Differentialgleichung r = k * C2
(suchen Sie einmal nach der
'geschlossenen' Lösung dieser Differentialgleichung!!)
In folgender Abbildung wird der Konzentrations-Verlauf der Komponente A
(Abklingkurve) in einer 'Echtzeitsimulation' (ausgeführt in
Agilent(ehemals Hp)-VEE) für eine solche Reaktion von erster und zweiter
Ordnung gezeigt.
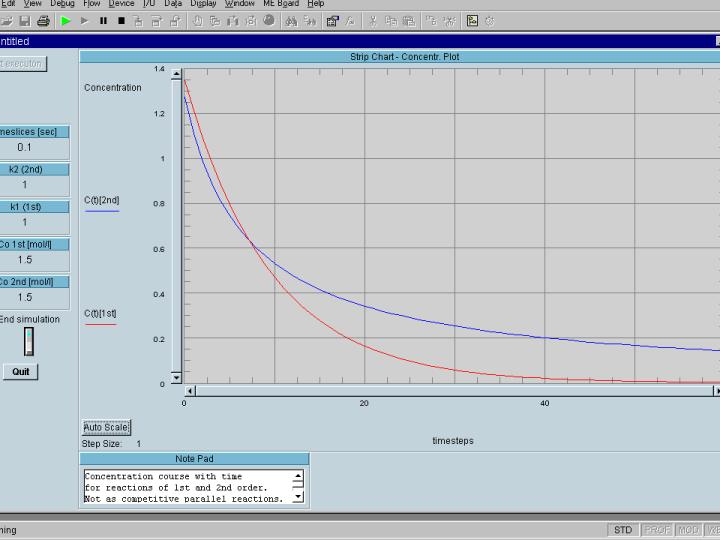
die rote Kurve entspricht der Reaktion 1. Ordnung, die blaue Kurve der
Reaktion 2. Ordnung.
Man sieht, daß bis zu einem 'Schnittpunkt' die Konzentation bei
einer Reaktion 2.Ordnung schneller abklingt, - nach dem Schnittpunkt aber
langsamer als die der Reaktion 1. Ordnung. Dies sieht man noch deutlicher im
nächsten Bild, in dem auch noch die momentanen Reaktionsgeschwindigkeiten
gezeigt werden.
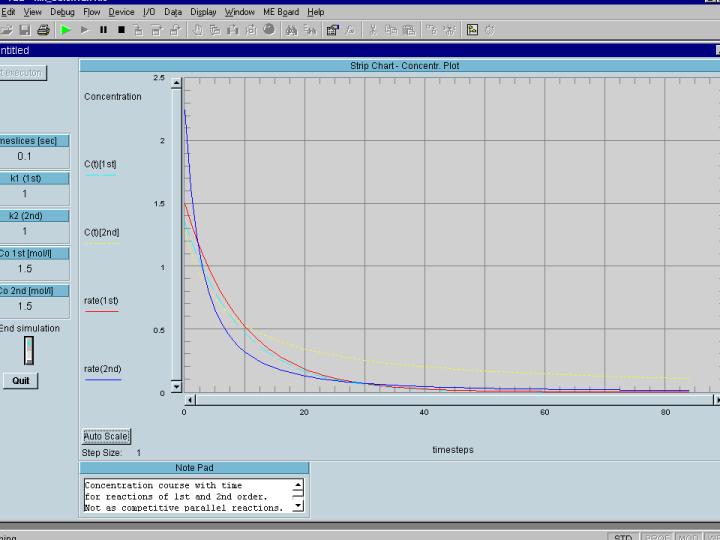
in dieser Abbildung sind die Konzentrationsverläufe für eine
Reaktion 1.Ordnung (hellblau) und für eine Reaktion 2.Ordnung (gelb),
sowie die Verläufe der momentanen Reaktionsgeschwindigkeiten für die
Reaktion 1. Ordnung (rot) und für die Reaktion 2.Ordnung (dunkelblau)
gezeigt. Die ersten beiden Kurven sind eine Wiederholung des obigen Bilds.
Man sieht in diesem Bild, daß die Reaktionsgeschwindigkeit der
Reaktion 2.Ordnung bis zum 'Schnittpunkt' über derjenigen für die
Reaktion 1.Ordnung liegt und danach kehren sich die Verhältnisse um. Woher
kommt das ? Können Sie sich das erklären ? eine kleine Hilfe:
diskutieren Sie die Funktion Y = X2 , am besten gleich verglichen
mit y = X1!!
Erklärung folgt
|
Da sich komplexere Reaktionsnetzwerke aus
Gleichgewichts-, Parallel- und Folge-Reaktionen zusammensetzen, wollen wir
diese Grundtypen von Reaktionen kurz besprechen. |
eine einfache Folgereaktion ohne reversible Teilschritte ist z.B.:
A
-> B -> C mit den Geschwindigkeitskonstanten k1 ('von A nach
B') und k2 ('von B nach C')
Als reaktionskinetische Ansätze kann man formulieren:
dcA/dt = -k1 cA
dcB/dt =
k1cA - k2cB
dcC/dt =
k2cB
aus der folgenden Abbildung für die Konzentrationsverläufe von
A,B und C sieht man, daß das Verhältnis k1/k2
dieselben deutlich erkennbar beeinflußt.
in der Abbildung sind: I = Komponente A, II = Komp. B, III = Komp. C.
Das Bild a.) gilt für k1 = k2, das Bild b.) für
k1 = 20 k2 und Bild c.) für k1 = 1/28
k2.
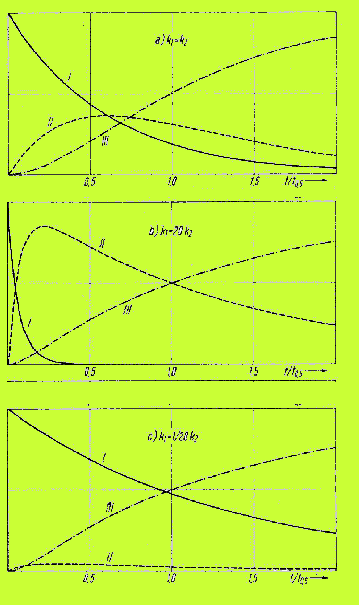
man sieht zusammenfassend: die Konzentration des Zwischenprodukts B hat
ein Maximum wenn k1 > k2 ist oder zumindest
k1 = k2 ist. Man sieht auch, daß man nur sehr wenig
B erhält, wenn k2 >> k1 ist. In diesem Fall
werden wir mit den reaktionstechnischen Mitteln der Konzentrationsführung
wenig Erfolg haben. Wir werden etwas in der 'Chemie' des Prozesses ändern
müssen, z.B. einen katalytischen Prozeß ausarbeiten, der die Bildung
von B begünstigt, oder es gelingt vielleicht, k1/k2
mit der Wahl der Reaktionstemperatur günstig zu beeinflußen.
Gleichgewichtsreaktionen
Man könnte die einfachste Gleichgewichtsreaktion A <-> B
salopp als Spezialfall der Folgereaktion A -> B -> A betrachten. Die
Ergebnisse einer kinetischen Betrachtung werden also nicht dramatisch anders
sein.
wir betrachten also: A <-> B mit
k1 (Hinreaktion) und k2
(Rückreaktion):
wenn wir mit cB,0 = 0 starten, wird B produziert bis der
Maximale Umsatz UA,max erreicht ist. Dieser ist festgelegt durch die
thermodynamische Gleichgewichtskonstante K = k2/k1. Um
den maximalen Umsatz zu berechnen, schreibt man:
rA =
-dcA/dt = k1 cA - k2
cB
und substituiert die Konzentrationen mit
UA:
cA =
cA,0(1-UA)
cB =
cB,0UA
aus der Geschwindigkeitsgleichung wird
dann:
dUA/dt = k1(1-UA) -
k2UA
im Gleichgewicht gilt:
für
UA,max: dUA/dt = 0
daraus
folgt:
UA,max =
k1/(k1+k2)
dies ist der Maximale Umsatz
zu B für diese Reaktion (also letztlich die Stelle Bmax in der
obigen Folgereaktion!!).
Was nützt uns das für eine
spätere Konzentrationsführung ? wir werden unsere Reaktion nur bis zu
der Reaktionsdauer laufen lassen können, die äquivalent zum maximalen
Umsatz ist.
Parallelreaktionen
ein sehr einfacher Fall einer Parallelreaktion ist: A - >B parallel
zu A -> C, eine irreversible Parallelreaktion. Die beiden Reaktionen sind
konkurrierend. Aus reaktionskinetischer Sicht entspricht das
Produktbildungsverhältnis dem Verhältnis der
Reaktionsgeschwindigkeiten der beiden konkurrierenden Zweige und damit der
Geschwindigkeitskonstanten und der Reaktionsordnungen derselben. Es
läßt sich formal herleiten:
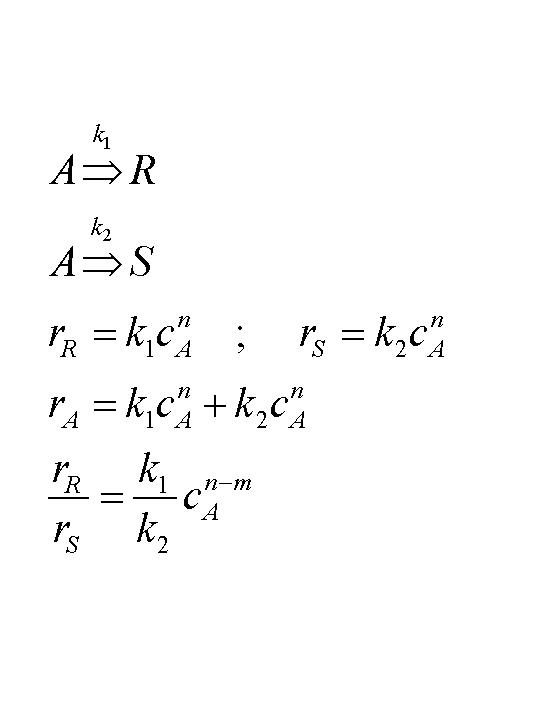
kinet. Gleichungen
einer einfachen Parallelreaktion
Für gleiche Reaktionsordnung beider Zweige, z.B. 1. Ordnung, also
mit n=m kann man herleiten:
| Größe |
Formel |
relative Produktkonzentration an B
cB/cA,0 |
cB/cA,0 = (
k1/(k1+k2) ) *
UA |
relative Produktkonzentration an C
cC/cA,0 |
cC/cA,0 = (
k2/(k1+k2) ) *
UA |
| Selektivität zu B SB |
SB = k1/(k1+k2) |
| Selektivität zu C SC |
SC = k2/(k1+k2) |
Produktverhältnis B zu C
cB/cC |
cB/cC = k1/k2 |
Der Fall unterschiedlicher Ordnungen muß diskret mit den
vorliegenden Daten diskutiert werden. Für eine Konzentrationsführung
spielt dabei immer die aktuelle Konzentration an A eine große Rolle.
Für die Konkurrenz niedriger (z.B. erster) Ordnung mit höherer (z.B.
zweiter) Ordnung gelten ähnliche Gesichtspunkte wie beim obigen Vergleich
nicht konkurrierender Reaktionen (y=X2 und Y=X1)
Die aufgeführten Beispiele sollten für die spätere
Besprechung der umsatzorientierten Optimierung oder der
Konzentrationsführung hilfreich sein. Einige wenige weitere
Ergänzungen folgen bald. Inzwischen geht's aber schon mal weiter:
Schaun wir einmal mit einem 'Mikroskop-Auge' hinein in einen Reaktor bis
'hinab' zu einem (gedachten) Reaktionsort (z.B. ein Würfel mit der
Kantenlänge von ein paar Molekülgrößen) an dem gerade
Moleküle zur Reaktion zusammentreffen. Nachdem Edukt-Moleküle zu
Produkt-Molekülen 'zusammengefunden' haben, sind in diesem Moment keine
neuen Eduktmoleküle da. Diese müssen erst durch Stofftransport
nachgeliefert werden.Wenn 'übliche' (nicht ultraschnelle) chemische
Reaktionen in gut durchmischter fluider Phase (Gas oder Flüssigkeit,
eventuell noch zusätzlich um-gerührt/-gewälzt) in Reaktoren von
Laborgröße ablaufen, dann ist in der Regel der stoffliche
Nachtransport von Reaktanden zum Reaktionsort viel schneller als die Reaktion
(zur Erinnerung: Brown'sche Molekularbewegung). Ja, - eine sogenannte
'homogene' Reaktion zeichnet sich ja gerade dadurch aus, daß keine
räumlichen Stoffverarmungen auftreten. Aber !! Die Physikalische Chemie
hat durchaus 'homogene' Reaktionen 'anzubieten' bei denen räumliche
Verarmungen aufgezeigt werden können. So kommen z.B. 'Oszillierende'
Chemische Reaktionen dadurch zustande, daß sogar in homogener Phase
örtlich (aber selbstverständlich auch zeitlich) unterschiedliche
Konzentrationen auftreten, die man dann manchmal auch durch Farbeffekte
erkennen kann. Bekannte Beispiele sind die Belousov-Zhabotinskii-Reaktion
(siehe z.B. : Angew. Chem. 90,1-16 (1978) ) und die Briggs-Rauscher-Reaktion
(siehe z.B. : J. Chem. Educ. 50, 496 (1973)). Wie so etwas zustande kommt, ist
etwas schwierig zu erklären: das Reaktionsnetzwerk führt zu einem
System verkoppelter reaktionskinetischer Differentialgleichungen (dynamische
Rückkopplungsmechanismen), das (im Konzentrationsverlauf)
'schwingungsfähig' ist., - also eigentlich sogar eine 'rein
formalmathematische' Sache, wie sie in der Physik in der Mechanik z.B. bei
Pendeln, in der Akustik und in der Wechselstromtechnik in ähnlicher Weise
zu beobachten ist. Wenn ich nun aber - allen ernstes - so ein Becherglas, in
dem eine solche oszillierende Raktion abläuft mit einem
ultra-high-speed-Rührer umrühre, kann ich es schaffen, den Effekt
zumindest örtlich gesehen zu 'beseitigen' (nicht unbedingt auch
zeitlich!!). Stellen wir uns dann andererseits einen Reaktionsapparat von
nahezu Kirchturmhöhe vor. Wenn wir in diesem Apparat eine Reaktion
'ungerührt/unumgewälzt' homogen durchführen, werden wir allein
schon durch 'Thermosyphoneffekte' und ähnliches eine nicht mehr so richtig
homogen durchmischte Reaktionsmasse im gesamten Reatorvolumen vorfinden.
|
Die Durchmischung der
Reaktionsmasse durch Stofftransportvorgänge hat einen großen
Einfluß auf die 'Homogenität' derselben. Da die
Reaktionsgeschwindigkeit durch die Komponentenkonzentrationen beeinflußt
wird, sind Konzentrationsunterschiede (Konzentrationsgradienten) im
Reaktionsraum von Einfluß auf die 'global' zu beobachtende
'Bruttoreaktionsgeschwindigkeit'. Die Frage der Vermischung der Reaktionsmasse
ist also von großer Bedeutung. |
|
Von apparativer Seite gesehen ist die im deutschen Sprachgebrauch von
mehreren 'Schulen' im Bereich der Technische Chemie benutzte Bezeichnung
'Makrovermischung' sehr wichtig. Hierunter
soll die im 'Makroskopischen Bereich' - salopp gesagt im Bereich, der mit dem
bloßen Auge beobachtet werden kann - herrschende Vermischung gemeint
sein. Für diese Vermischung können wir zwei Grenzfälle
postulieren:
- die 'vollständige Vermischung' ( oder 'vollständige Rückvermischung'), bei der mit
dem Auge keine Inhomogenitäten beobachtet werden können.
- die 'vollständige Nicht-Vermischung' (oder 'vollständige Nicht-Rückvermischung'), - wo
das Auge (natürlich nur unter bestimmten Voraussetzungen, also:
theoretisch) streng abgegrenzte Bereiche 'sieht'.
Zwischen diesen beiden Grenzfällen liegt nun in der Praxis ein
bestimmter 'Grad an Rückvermischung'. Nehmen wir nun zum Beispiel einmal
den Idealreaktor AIK. Von diesem wissen wir schon, und wir müssen es jetzt
ja nur noch nach der soeben getroffenen 'Nomenklatur' ausformulieren: er ist
(räumlich) 'vollständig rückvermischt'. Dasselbe gilt auch
für den KIK (klar?). Wie sieht es nun aber für den idealen
Rohrreaktor aus? Da können wir vorsichtigerweise vielleicht lieber von der
Defintion ausgehen: jedes der 'Fluidelemente' = Scheibchen steht nicht im
Stoffaustausch mit seinen Nachbarn. Das ist nach unserer 'Nomenklatur':
'vollständig Nicht-Rückvermischt'
|
AIK und KIK sind
räumlich vollständig rückvermischt, das IR ist vollständig
nicht-rückvermischt. Die Idealreaktoren repräsentieren die
Grenzfälle der Rückvermischung. |
|
Nochmals, - ist Ihnen klar, warum der Grad der Rückvermischung
wichtig für das Reaktionsergebnis ist ? Nein ? Dann stellen Sie sich einen
Reaktionspott vor, bei dem 'in der einen Ecke' kaum noch Edukte zu finden sind,
in der 'anderen Ecke' es 'davon geradezu wimmelt'. In der eduktarmen Zone wird
in der Regel die Reaktionsgeschwindigkeit sehr niedrig sein, - da tut sich
'fast nichts mehr'. Im Gegensatz dazu die andere Ecke !!!
Kann man nun durch Experimente oder Berechnungen etwas über die
Rückvermischung in Reaktionsapparaten erfahren ? Wir haben doch bei der
Beschreibung der Begriffe Makrovermischung und Rückvermischung von der
'Beobachtung mit dem Auge' gesprochen. Wäre es nicht denkbar, daß
wir durch Färbeversuche Infos erhalten könnten (denken Sie doch
beispielsweise an die Unterwasserhöhlenforschung). Man spricht dann von
Farb-Tracern. Na ja, und wenn Farbtracer funktionieren, könnte es auch mit
anderen Tracern, wie radioaktiven Stoffen u.v.a. gehen!! Und hier sind wir
genau an der Überleitung zum 'Verweilzeitverhalten' von Reaktoren.
|
Das
Verweilzeitverhalten eines Reaktors charakterisiert sein Makromisch -
Verhalten |
|
Diese Charakterisierung des Makromischverhaltens wird im
anglosächsischen sehr treffend mit 'contacting pattern' (also
Kontaktierungsmuster) bezeichnet: the Residence Time behaviour of a reatcor
characterizes it's contacting pattern.
Aber da wir oben vom Begriff Makrovermischung gesprochen haben, werden
wir auch noch über den Begriff 'Mikrovermischung' sprechen
müssen. Was wollen wir unter diesem Begriff verstehen ? Na ja, um
konsequent zu bleiben, sollten wir damit alles im 'mikroskopischen' bis
'submikroskopischen' Bereich meinen. Und das tun wir auch !! Wir wollen unter
einem 'vollständig mikrovermischten
Fluid' einfach ein 'molekulardisperses' System verstehen, z.B. eine
Zuckerlösung oder Kochsalzlösung. Was wäre dann aber ein
vollständig 'nicht-mikrovermischtes
Fluid'? Lassen Sie uns hierunter ein Fluid aus mikroskopisch kleinen
Elementen, wie z.B. Kügelchen verstehen, die keinen stofflichen Austausch
mit ihren Nachbarn haben. Man könnte hier als Modell auch einen 'Schwarm'
mikroskopisch kleiner AIKs annehmen. Man nennt diesen 'Getrenntsein-Zustand'
auch 'vollständige Segregation'. Nun,
das ist ja ein 'ganz nettes' Modell, aber gibt es so etwas auch (wenigstens
andeutungsweise) in der Realität? -- Denken Sie doch einmal an
Milchtröpfchen-Emulsionen !! Emulsionen sind ein gutes Praxisbeispiel
für segregierte Fluide. Klar, ist der Zustand einer vollständigen
Segregation wieder eine 'Idealsache', aber man kann bei partiellem
Stoffaustausch (Koaleszenz und Tröpfechenneubildung) ja dann von einem
'individuellen' Segregationsgrad sprechen.
|
Vollständige
Mikrovermischung (volldisperses oder molekulardisperses System) und
vollständige Segregation (z.B. ideale Emulsion) sind mikroskopische
Eigenschaften eines Fluids. |
|
Im Normalfall hat der Reaktor keinen Einluß auf den Zustand der
Mikrovermischung. Theoretisch wäre natürlich ein Fluid, das durch
einen idealen Rohrreaktor fließt, ein segregiertes Fluid ( dies eben
'automatisch' wegen der differentiell kleinen Scheibchen!!). Aber das IR
gibt es nicht. Außerdem fallen hier der
'Makrovermischungsbegriff vollständig
nicht-rückvermischt' und der 'Mikrovermischungsbegriff
vollständig segregiert' sozusagen zusammen. Praktisch gesehen ist
der Rohrreaktor aber einfach in einem hohen Maß
'nicht-rückvermischt' und diese seine Eigenschaft hat aber nichts mit den
Fluideigenschaften im Mikrovermischungsbereich zu tun, das Fluid kann
molekulardispers oder segregiert sein. Das sind aber mehr oder weniger
Formalismen.
Daß die Makrovermischung im Reaktor eine relevante Sache
ist, kann man einsehen, - aber hat die Mikrovermischung auch praktische
Bedeutung? Meine Antwort: sie hat sehr viel weniger Bedeutung, aber bei
Reaktionen mit Elmulsionen, Dispersionen und ähnlichen Fluiden kann der
Zustand der Mikrovermischung schon einmal reaktionstechnische Bedeutung
erlangen (Hauptgebiet Makromolekulare Chemie - z.B. Emulsionspolymerisationen
!!). Kann man den Mikrovermischungszustand (vollständige) 'Segregation'
irgendwie visualisieren, wenn man ihn doch mit dem bloßen Auge gar nicht
sieht ?
Im Falle vieler segregierter Fluide kann man mit Hilfe des
Tyndall-Streu-Effekts aufzeigen, daß 'nicht-molekulardisperse' Systeme
vorliegen, also Segregation sozusagen 'sichtbar machen'.
Schließlich muß hier noch einiges zur Nomenklatur im
Anglosächsischen und auch an verschiedenen 'Europäischen Schulen'
gesagt werden, damit keine Verwirrung entsteht !
Häufig - vor allem im
Anglosächsischen - wird der Segregationszustand als 'Makrovermischtes
Fluid' oder besser 'Makrofluid' bezeichnet. Gegen letztere Benennung ist
eigentlich nichts einzuwenden. Es wäre dann eben Mikrofluid =
molekulardispers und Makrofluid = segregiert. Die 'Anwender'
dieser Nomenklatur haben dann aber keine treffenden Benennungen mehr für
den Vermischungszustand, den wir als 'mit dem Auge sichtbaren
Makrovermischungszustand' bezeichnen. Die Anglosachsen helfen sich dann mit dem
(meiner Meinung nach auch sehr treffenden) Begriff 'contacting pattern' aus,
der aber nicht so 'universell' ist, - und sie sprechen dann eben im weiteren
von back-mixed und not-backmixed. Irgendwie geht das auch, ich persönlich
finde aber eben die Kategorisiereung in 'Makrovermischung' und
'Mikrovermischung' mit den jeweiligen 'Unterschubladen'
vollständig und vollständig-nicht als
logisch und systematisch. Für Sie als Leser ist halt wichtig, jeweils zu
ergründen, was der betreffende Autor meint, denn letztlich ist alles
Definitionssache, denn die Phänomene sind natürlich nicht verschieden
(weil die Naturwissenschaftler ja leider nicht
'die Bestie Natur bezwingen'
können !)
pdf-Datei des vorliegenden
Teils 2 (ca. 560 k), Feb. 2009
weiter zu Teil 3
weiter zu Teil 4
zurück zu Teil 1
zur
Homepage des Autors
Bitte teilen Sie mir mit, wenn ein Interesse am vorliegenden Stoff
besteht ! Ganz toll wäre auch, wenn ich auf Fehler aufmerksam gemacht
würde.