Über die Entwicklung meiner Echtzeitsimulationen

Zeit- und Amplituden-'Quantisierung'

Zeitabhängige Prozesse beschreiben normalerweise den Verlauf von 'stetigen' Analogwerten mit der 'kontinuirlichen' Zeit. Digitale Elemente, wie Mikro-Prozessoren, -Controller und digitale Schaltkreise arbeiten 'stufenweise' sowohl im 'Variablenwert' als auch in der Zeit, d.h. sie führen eine 'stufenweise Quantisierung' der 'zuvor' analogen Werte durch. Die Zeitquantisierung wird z.B. bei Mikroprozessoren geprägt durch die Prozessor-Taktzeit und allgemein in digitalen Schaltelementen durch den angelegten Zeit-Takt. Wie Sie vom Computer her wissen, ist die Genauigkeit von Variablenwerten von der Bitbreite des digitalisierten Werts abhängig ( 8 Bit, 16 Bit, 32 Bit und mehr). Sie wissen auch, daß die Rechengeschwindigkeit von der CPU-Taktzeit abhängt. Dies ist die Basis aller numerischen Näherungen von zeitabhängigen analogen Vorgängen mit Hilfe der Digitaltechnik. Es ist deshalb einleuchtend, daß die 'stufenweise Behandlung' von 'zeitstetigen' Vorgängen nur dann genau genug sein kann, wenn die digitale Taktzeit sehr kurz ist im Vergleich zur Gesamtzeit des Prozesses ('Eigenzeit'). Das Shannon-Theorem besagt als Regel, daß die Taktfrequenz mindestens 10 mal höher sei sollte, als die 'schnellste' Frequenz im analogen Vorgang. Soviel zur 'Zeitquantisierung'. Die 'Amplituden-Quantisierung' und ihre Genauigkeit dürfte Ihnen im heutigen Zeitalter der Computer geläufig sein !

Die Entwicklung einer Simulation:

der reale Prozess: irgendwelche 'Potentialgrößen' laufen mit der Zeit ab, - sie könnten experimentell beobachtet werden, oder man weiß (kennt) die Gesetzmäßigkeit des Ablaufs.

man macht sich ein Modell, das beschreibt, wie der Prozess verläuft.

Man entwickelt eine 'Bilanzgleichung' oder allgemeiner eine formalmathematische Beschreibung für die betrachteten Variablen (z.B. Temeperatur, Druck, Kraft, Weglänge, Stoff - Bilanz --->

dies führt in den meisten Fällen zu einer zeitlichen Differentialgleichung der Form:

dy/dt = f(y)

man wendet die Methode der 'logistischen Gleichung' an: der Differentialquotient dy/dt wird ersetzt durch den Differenzenquotienten für 'Scheibchen-Zeiten' << 'Prozess-Eigenzeit'

entwickle ein Rechnerprogramm mit in der Zeit zyklischer Struktur ('oncycle') unter Verwendung hierfür geeigneter Software (z.B. HP/Agilent-VEE)

visualisieren in einem Graphen oder Daten abspeichern.

Die Logistische-Gleichung-Methode .

Diese Methode ist sozusagen die Umkehr des Übergangs vom Differenzenquotienten zum Differentialquotienten in der Mathematik, - d.h. wir gehen zurück vom infinitesimalen Wert dt = 0 zu sehr kleinen Wert 'delta t' nicht gleich 0, aber eben klein im Vergleich zur Eigenzeit, - dies ist der Differenzenquotient. Nehmen wir ein einfaches Beispiel aus der Chemie: die kinetische Gleichung einer einfachen Reaktion 1. Ordnung:

dc/dt = k*c

ersetzen wir den Differentialquotienten durch den Differenzenquotienten:

delta(c) / delta (t) = k*c
delta(c) = k*c*delta(t)

mit: delta(c) = c_j+1 - c _j ,
wobei j +1 = Index für den 'neuen Zeitschritt-Wert' und j = derjenige des 'Zeitschritts davor' sein soll.
man erhält dann:

c_j+1 = c_j*(k*delta(t) + 1)

Diese algebraische Gleichung nennt man Logistische Gleichung und mit im Vergleich zur 'Eigenzeit' sehr kleinen Zeitschritten kann diese Methode stetige analoge Prozesse recht ordentlich 'annähern'. Digitale Systeme sind 'prädestiniert' für diese Form von Gleichungen, denn sie arbeiten 'von Natur aus' in einer Zeit- und Amplituden-Quantisierung. Das merkt man auch, wenn man programmiert: Sie müssen für Variablen Rekursionsschleifen (zum Beispiel in C-Code: i++ = 1 ). Die Werte werden dabei je Zeitschritt um einen kleinen Betrag in(de-)krementiert. Die Methode der Logistischen Gleichung wird sehr gut im Buch von Manuel Jakubith, Grundoperationen und chemische Reaktionstechnik (Wiley-CH ) beschrieben. Man findet dort zum Beispiel für Differentialgleichungen erster und zweiter Ordnung:

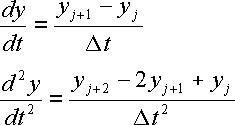
ein weiteres Beispiel: Mechanik, die beschleunigte Bewegung

nehmen Sie die 'browser back' Funktion zur Rückkehr zum vorhergehenden Text oder:

zur Hauptseite