Etwas ausführlicher: die Kalorik- (Kalorimeter)-Formel

Machen wir uns ein Beispiel für die Wärmeübertragung anhand der Kalorik-Formel (siehe hierzu auch Lehrbücher der Physik!!):

Nehmen wir einmal an, wir hätten einen Metallblock von bekannter Masse (z.B. 1kg). Dieser habe eine Temperatur von 25 ⁰C. Wir erwärmen diesen Block nun in einem Wärmebad mit einem 'riesigen Wärmevorrat' bei einer Temperatur von 40 ⁰C. Der an den Metallblock vom Wärmebad übertragene Energieinhalt = die an ihn übertragene Wärme(-menge) ist dann:

Q = m × c × Δ T
und im Beispiel:
Q = 1 × c × (40-25)
-------- > (Energie-Einheiten, z.B. Watt oder cal) ;

vom c-Wert nehmen wir im Moment einfach mal an, er sei bekannt (da wird es schon einen Weg geben, diesen zu ermitteln ---> z.B. Wärme-Mischungsversuche im Kalorimeter)

Könnten Sie jetzt folgende Aufgabe lösen ?

1 kg Wasser von 25 ^oC wird mit 2 kg Wasser von 48 ^oC gemischt, welche Temperatur hat die Mischung ?

viel Erfolg !!!

Berechnung der 'Mischtemperatur' mit der Kalorimeter-Formel

Wenn wir zwei Körper 'mit begrenztem' Wärmeinhalt miteinander in Kontakt bringen, also z.B. zwei Festkörper, oder wir 'tauchen' einen Festkörper in ein Fluid, - dann wird solange Wärme vom wärmeren Körper auf den kälteren übertragen bis beide Wärmeinhalte gleich sind. In beiden Körpern wird dann die Misch-Temperatur (Ausgleichstemperatur) erreicht. Diese kann mit Hilfe der Kalorimeter-Formel berechnet werden:

Q₁ = m₁ × c₁ × (T₁-T_m)

Q₂ = m₂ × c₂ × (T_m-T₂)

Q₁= Q₂

m₁ × c₁ × T₁ - m₁ × c₁ × T_m = m₂ × c₂ × T_m - m₂ × c₂ × T₂

m2 × c₂ × T_m + m₁ × c₁ × T_m = m₁ × c₁ × T₁+ m₂ × c₂ × T₂

T_m = (m₁ × c₁ × T₁ + m₂ × c₂ × T₂) / (m₂ × c₂ + m₁ × c₁)

hierbei sind: Q₁ von Stoff 1 abgegebene Wärme (also 1 = wärmer , 2 = kälter) ; Q₂ von Stoff 2 aufgenommene Wärme ; c₁, c₂ = spezifische Wärmen der beiden Stoffe ; m₁, m₂ = Massen der beiden Stoffe ; T₁, T₂ Ausgangstemperaturen der beiden Stoffe ; T_m = erreichte Mischtemperatur

Dies ist eine der wichtigsten Anwendungen für die bekannte 'kalorimetrische Formel', die jeder Physik- und Chemie-Student kennen sollte.

Die Formel ist zugleich die formale Lösung der Aufgabe im vorherigen Abschnitt.

zurück !!

Intuitive Herleitung des Fourier-Gesetzes

Eine elegante Vorgehensweise ist nun darüberhinaus, wenn man für die zwei Wärmevorratsblöcke den Vorgang der latenten Wärmebindung oder Wärmefreisetzung anwendet, also z.B. siedendes Wasser auf der einen Seite und schmelzende Eiswürfel auf der anderen. Dies bedarf zwar an dieser Stelle einiger Erklärung, aber es rentiert sich!!.
Latente Wärmen sind Phasenumwandlungswärmen. Es ist eine ganz besondere physikalisch-chemische Eigenschaft von Stoffen, daß bei Phasenumwandlungen, z.B. beim Schmelzen von gefrorenem Wasser (Eis) oder beim Sieden von Wasser immer ganz definierte Wärmemengen gebunden oder frei werden und daß sich bei diesem Vorgang die momentane Temperatur des Stoffes nicht ändert. Also: Eis schmilzt bei Wärmezufuhr bei konstant 0 ^oC, solange, bis alles Eis geschmolzen ist, - erst dann kann sich die Wassertemperatur erhöhen. Bei siedendem Wasser ist es das gleiche: Sie können heizen, wie Sie wollen, das Wasser verdampft und überschreitet dabei die Siedetemperatur (luftdruckabhängig!!) von z.B. 100 ^oC 'partout' nicht. Nun ist als Konsequenz dieser Verhaltensweise die Menge des geschmolzenen Eises oder die Menge verdampften siedenden Wassers ein direktes Maß für die zugeführte oder abgeführte Wärme. Diese Verhaltensweise gilt ganz allgemein für latente Wärmen.

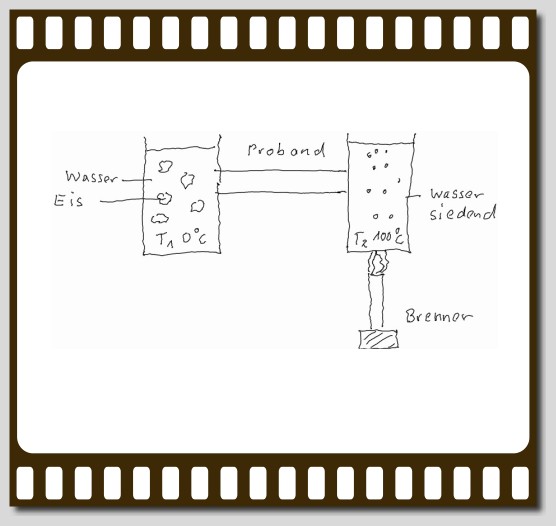
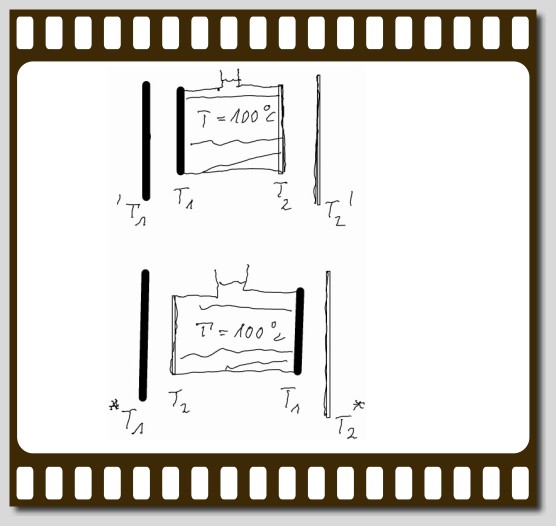
zur Erinnerung: Leitbrücken-Anordnung zur Wärmeleitfähigkeitsmessung unter Verwendung 'latenter' Wärmen

Atomistisch kann man sich das so interpretieren, daß im Regime (Bereich) der Phasenumwandlung einfach alle zur Verfügung stehende Energie ins 'Umwandeln' , z.B. aus der Flüssigkeit in den Gaszustand oder für den Einbau in ein Kristallgitter usw., 'gesteckt werden muß'.

Mit dieser Kenntnis gerüstet können wir uns jetzt anhand unserer Quellen-/Senken-Anordnung das Fourier-Gesetz der Wärmeletung plausibel machen.

Oder noch besser, überlegen wir uns doch zunächst mal, ob wir das Grundgerüst des Fourier-Gesetzes 'mit dem gesunden Menschenverstand' herleiten können.

Die pro Zeiteinheit über die Küvette 'durchgeleitete' Wärmemenge Q/t ist proportional zur Temperaturdifferenz ΔT (treibende Kraft). Sie wird auch proportional zur Querschnittsfläche der Küvette sein, denn je größer diese ist, desto mehr 'geht durch'. Schließlich wird sie um so größer sein, je kürzer die Küvette ist oder umgekehrt um so kleiner sein, je länger die Küvette ist. Das ist eine umgekehrte (reziproke) Proportionalität !! Kommt Ihnen das nicht bekannt vor ? Das ist doch wie beim elektrischen Widerstand eines Drahtes !! Na ja, was fehlt uns denn jetzt noch, -wie immer !! Eine Größe, die die spezifische Eigenschaft des vorliegenden Stoffes charkterisiert. Die nennen wir spezifische Wärmeleitfähigkeit . ( Wir hätten natürlich genauso einen reziprok proportionalen Wärmeleitungs-Widerstandswert definieren können !!).
Und Sie glauben es nicht, wir haben soeben das Fourier-Gesetz hergeleitet !!

es lautet:

Q/t = F × 1/L × λ × ΔT

zurück!!!

Kennzahlen / die Reynolds-Kennzahl

Die Reynolds-Zahl ist eine sogenannte 'dimensionslose Kenngröße'. Sie erlaubt, in fluiden Strömungs-Systemen zu beurteilen, ob man sich im Regime der laminaren oder turbulenten Strömung befindet.
Dimensionslose Kennzahlen und deren Zusammenhänge sind ein 'Produkt' der Ähnlichkeitstheorie. Ihre Anwendung ist in vielen Gebieten von Physik, Physikalischer Chemie und vor allem Ingenieurwesen weit verbreitet.

Falls Sie über dimensionslose Kennzahlen etwas mehr grundsätzliche Information benötigen, hier ein Textblock, den ich aus 'Patat-Kirchner - Lehrbuch der Technischen Chemie' abgeschrieben habe: (überspringen !)

Grundlagen der Ähnlichkeitslehre.
Die Ähnlichkeitslehre oder Theorie der dimensionslosen Kenngrößen baut sich auf dem Begriff der Ähnlichkeit der elementaren Geometrie auf. Zwei Rechtecke sind einander ähnlich, wenn das Verhältnis von Länge u Breite bei beiden gleich ist. Das Verhältnis zweier Längen ist, wenn sie in der gleichen Einheit gemessen sind, unabhängig von der Art des benutzten Maßsystems und der Einheit. Ferner ist es dimensionslos, und man bezeichnet es deshalb auch als dimensionslose Kenngröße oder dimensionsloses Produkt. Die notwendige und hinreichende Bedingung für die geometrische Ähnlichkeit zweier Rechtecke ist also, daß zwei dimensionslose Zahlen gleich sind. Bei physikalischen und chemischen Prozessen sind neben der Länge noch weitere Grundgrößen, z.B. die Zeit, von Einfluß und damit Einflußgrößen. Neben den Grundgrößen können aber auch abgeleitete Größen für einen betrachteten Vorgang maßgebend sein. Solche Einflußgrößen sind beispielsweise Kraft bzw. Masse, Geschwindigkeit, Druck, Zähigkeit. Sie lassen sich immer auf Grundgrößen, präziser gesagt auf Potenzprodukte von Grundgrößen, zurückführen.

Um nun das Ähnlichkeitsprinzip auf Einflußgrößen physikalischchemischer Vorgänge anzuwenden, geht man im allgemeinen folgendermaßen vor: Man überlegt zuerst alle Einflußgrößen, die für einen betrachteten Vorgang maßgebend sein könnten. Dann schreibt man diese Einflußgrößen und ihre Dimensionen auf und versucht, aus ihnen durch geeignete Multiplikationen und Divisionen Produkte und Quotienten zu bilden, die dimensionslos sind. Sind alle Einflußgrößen zu dimemionslosen Kenngrößen zusammengefaßt, so sollen zwei physikalische Vorgänge einander ,,ähnlich“ sein, wenn alle entsprechenden Kenngrößen bei beiden Vorgängen dieselben Werte haben.

Die Reynoldszahl :

Ganz allgemein kann gezeigt werden, daß 'reibende' Strömungen um geometrisch ähnliche Körper dann ähnlich verlaufen, wenn die dimensionslose Größe:

in zwei ähnlich gelegenen Punkten den gleichen Betrag hat. L ist dabei eine charakteristische Länge, wie Durchmesser (z.B. bei Rohrströmungen), Flügeltiefe (von Propellern, Laufrädern etc.) u.ä.
w ist die lineare Strömungsgeschwindigkeit.
Es läßt sich zeigen, daß die so definierte Reynolds-Zahl ein Maß für das Verhältnis der Trägheitskräfte zu den Zähigkeitskräften im strömenden Fluid ist.

Charakterisierung der Strömungs-Regime durch die Reynolds-Zahl:

Text folgt !!

zurück !!!

Kennzahlenzusammenhänge zur Ermittlung von Wärmeübergangskoeffizienten

Für die Berechnung des Wärmeübergangskoeffizienten α werden Kennzahlenzusammenhänge der folgenden Kennzahlen verwendet:
Nu = Nusselt, Pr = Prandtl, Re = Reynolds und Gr = Grashof

Wenn man die Einflußgrößen auf α beim Wärmeübergang zusammenstellt, kann man eine allgemeine Funktion der folgenden Form annehmen:

hierbei ist L die bei der Reynoldszahl schon erwähnte charakteristische Länge, Cp die spezifische Wärme, dg eine geometrische Apparateabmessung (z.B. dlie Gesamtlänge einer Wärmetauscherplatte), w die Lineargeschwindigkeit, eta die dyn. Viskosität und rho die Dichte. Aufgrund der Ähnlichkeitstheorie läßt sich diese Funktion in Form von dimensionslosen Produkten darstellen:

wobei:

Nu = Nusselt, Pr = Prandtl
die 3. Kennzahl ist die bereits bekannte Reynoldszahl und die 4. Kennzahl eine 'Geometrie'-Kennzahl

man kann nun bei Verwendung algemeiner Ansätze der Form:

mit experimenteller Hilfe die in Frage kommenden Exponenten ermitteln und aus der erhaltenen Nu-Kennzahl α 'berechnen'.

Bei freier Konvektion tritt dagegen an Stelle der Reynoldszahl die Grashof-Zahl Gr 'in Aktion'. Diese brücksichtigt eben die Fluidbewegungen bei freier Konvektion (Umschichtung, 'Thermik' ). Man erkennt dies schön an den in der Grashoffzahl vorkommenden Einflußgrößen g (Erdbeschleunigung), β=thermischer Ausdehnungskoeffizient und Δ-T.

der Zusammenhang hat die allgemeine Form:

zurück !!!

der k-Wert

Formel der Widerstands-Serienschaltung beim Wärmedurchgang. Zur Wiederholung: die 3 Terme im Nenner sind 'Wärmeübergang auf Seite 1' , 'Wärmeleitung durch die Wand' , 'Wärmeübergang auf Seite 2'.

zurück !!

Informative Versuchsanordnung für Übertragung durch Strahlungswärme: Leslie-Versuch

Beim Leslie-Versuch ist ein auf konstante Temperatur (nur z.B. 100 ^oC) gebrachter Würfel zwischen zwei Platten angeordnet. Oberer Abbildungsteil: der Würfel besitzt eine schwarze Wandfläche und eine polierte oder blanke Fläche. Die Emissionstemperatur der schwarzen Fläche ist T1, die der blanken T2. Gegenüber den Würfelflächen ist eine schwarze Platte angeordnet, die eine Absorptionstemperatur T'₁ erreicht. Auf der gegenüberliegenden Seite befindet sich (wiederum gegenüber der blanken Würfelfläche) eine blanke Platte, die die Absorptionstemperatur T'₂ annimmt. Unterer Abbildungsteil: der Würfel wird dann gedreht, so daß der schwarzen Platte die blanke Würfelseite und der blanken Platte die schwarze Würfelseite gegenüber steht. Die schwarze Platte nimmt jetzt die Temperatur T*₁ und die blanke Platte die Temperatur T*₂ an.

der Leslie-Versuch

In der oberen Anordnung wird die Temperatur T'₁ der schwarzen Platte wesentlich größer sein als die (T'₂) der blanken Platte, - dies bedeutet, daß das Emissions- und Absorptionsvermögen schwarzer Körper am größten ist.
In der unteren Anordnung kann beobachtet werden, daß die Temperaturen T*₁ und T*₂einander gleich sind, die Wärmeflüsse sind hier also gleich. Hieraus lässt sich herleiten, daß die Verhätnisse des Emissionsvermögens zum Absorptionsvermögen von blanker und schwarzer Fläche einander gleich sind: E₁/A₁ = E₂/A₂.

zurück !!

Strahlungswärme-Übertragung zwichen 2 Platten (Patat-Kirchner)

für die Wärmeübertragung zwischen 2 Platten, die sich auf den Temperaturen T₁ und T₂ befinden, läßt sich herleiten:

Herleitung siehe z.B. 'Patat-Kirchner'. Charakteristisch für die Wärmeübertragung durch Strahlung ist der Term 'T⁴' (Stefan-Boltzmann-Gesetz).
Man könnte salopp sagen: bei der Strahlungswärme ist der 'Potentialeffekt' der Temperatur 'gewaltig'.

zurück !!